隨著新課程改革的不斷深入，如何促進(jìn)學(xué)生深度學(xué)習(xí)，培養(yǎng)學(xué)生創(chuàng)新思維是教育研究者一直探索的問題。本文以“離散型隨機(jī)變量及其分布列”教學(xué)為例，闡釋了通過(guò)“創(chuàng)設(shè)情境→質(zhì)疑思辨→合作探究→展示提升→反思悟道”等五環(huán)創(chuàng)新思維課堂教學(xué)模式，以促進(jìn)學(xué)生的深度學(xué)習(xí)。

教師要關(guān)注學(xué)生的個(gè)性化發(fā)展，深入挖掘?qū)W科育人的價(jià)值，創(chuàng)設(shè)合適的教學(xué)情境，啟發(fā)學(xué)生進(jìn)行深度思考。實(shí)踐證明，高中數(shù)學(xué)課程更關(guān)注學(xué)生數(shù)學(xué)能力和思維能力的培養(yǎng)，重視對(duì)知識(shí)的深層理解和思想方法的掌握，從而實(shí)現(xiàn)真正意義上的知識(shí)構(gòu)建。這些要求正好與深度學(xué)習(xí)的理念相吻合，因此教師要重視學(xué)生的深度學(xué)習(xí),以提高教學(xué)效果。

一、對(duì)深度學(xué)習(xí)的認(rèn)識(shí)

“深度學(xué)習(xí)”概念來(lái)源于人工神經(jīng)網(wǎng)絡(luò)的研究。本文所說(shuō)的深度學(xué)習(xí)是以數(shù)學(xué)學(xué)科核心內(nèi)容為載體，以提升學(xué)生的思維品質(zhì)與數(shù)學(xué)素養(yǎng)為目標(biāo)，引發(fā)學(xué)生的認(rèn)知沖突，調(diào)動(dòng)他們?nèi)硇膮⑴c活動(dòng)，促使學(xué)生體驗(yàn)成功，獲得發(fā)展。特征是：第一，聯(lián)想與結(jié)構(gòu)（創(chuàng)設(shè)情境）——經(jīng)驗(yàn)與知識(shí)相互轉(zhuǎn)化，幫助學(xué)生喚醒并更新經(jīng)驗(yàn)，建構(gòu)知識(shí)體系，形成知識(shí)網(wǎng)絡(luò)。第二，活動(dòng)與體驗(yàn)（質(zhì)疑思辨）——學(xué)習(xí)機(jī)制，引導(dǎo)學(xué)生主動(dòng)學(xué)習(xí)，親身經(jīng)歷知識(shí)發(fā)現(xiàn)、形成、發(fā)展的過(guò)程。第三，本質(zhì)與變式（合作探究）——知識(shí)的加工，就是把握知識(shí)本質(zhì)的過(guò)程，或是質(zhì)疑探究，或是情境體驗(yàn)。第四，遷移與應(yīng)用（展示提升）——知識(shí)的外化，激發(fā)學(xué)生實(shí)現(xiàn)知識(shí)的拓展和應(yīng)用，將所學(xué)知識(shí)轉(zhuǎn)化為綜合實(shí)踐能力。第五，價(jià)值與評(píng)價(jià)（反思悟道）——人的成長(zhǎng)，是幫助學(xué)生思考所學(xué)知識(shí)在知識(shí)體系中的地位與作用、優(yōu)勢(shì)與不足。

二、教學(xué)策略示例

1.創(chuàng)設(shè)情境，尋找創(chuàng)新思維素材

情境1：超市在國(guó)慶期間舉辦憑購(gòu)物小票抽獎(jiǎng)的活動(dòng)。活動(dòng)道具：紙箱一個(gè)，5個(gè)相同大小的球，上面標(biāo)有數(shù)字1、2、3、4、5。獎(jiǎng)項(xiàng)設(shè)置：一等獎(jiǎng)、二等獎(jiǎng)、三等獎(jiǎng)。抽獎(jiǎng)規(guī)則：抽獎(jiǎng)?wù)邚募埾渲邢群竺鰞蓚€(gè)球，以兩個(gè)球上的數(shù)字之和作為獲獎(jiǎng)依據(jù)。請(qǐng)你根據(jù)超市提供的道具和要求，為其設(shè)計(jì)一個(gè)抽獎(jiǎng)方案。

設(shè)計(jì)意圖：以生活實(shí)例創(chuàng)設(shè)情境，搭建深度學(xué)習(xí)平臺(tái)，在問題的解決過(guò)程中，從映射與函數(shù)的角度逐漸形成“離散型隨機(jī)變量分布列”的概念，完成對(duì)“隨機(jī)變量分布列”概念的理解，進(jìn)而強(qiáng)化“離散型隨機(jī)變量”的概率分布對(duì)于刻畫隨機(jī)現(xiàn)象的重要性。

方案1：所獲獎(jiǎng)項(xiàng)為[Y]，設(shè)[Y]=1=一等獎(jiǎng)=[X]=10，[Y]=2=二等獎(jiǎng)=[X]=9，[Y]=3=三等獎(jiǎng)=[X]=8，[Y]=0=不中獎(jiǎng)=[X]=2，或[X]=3或[X]=4或[X]=5或[X]=6或[X]=7。

點(diǎn)評(píng)：方案1中，雖考慮到了獎(jiǎng)項(xiàng)設(shè)置的預(yù)期，但對(duì)其他隨機(jī)變量所對(duì)應(yīng)的概率沒有考慮，所以方案設(shè)計(jì)欠缺合理性。

方案2：所獲獎(jiǎng)項(xiàng)為[Y]，設(shè)[Y]=1=一等獎(jiǎng)=[X]=2或[X]=10，[Y]=2=二等獎(jiǎng)=[X]=3或[X]=9，[Y]=3=三等獎(jiǎng)=[X]=4或[X]=8，[Y]=0=不中獎(jiǎng)=[X]=5或[X]=6或[X]=7，如表格：

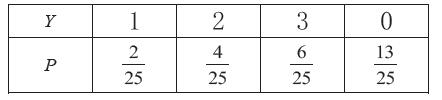
點(diǎn)評(píng)：方案2中，顯然考慮到了所有隨機(jī)變量所對(duì)應(yīng)的概率，所以設(shè)計(jì)比較合理。

設(shè)計(jì)意圖：通過(guò)不同方案的對(duì)比，讓學(xué)生意識(shí)到要想設(shè)計(jì)一個(gè)比較合理的方案，需對(duì)隨機(jī)變量的概率分布規(guī)律要有整體把握，即需建立隨機(jī)變量的取值與其概率的對(duì)應(yīng)，為分布列概念的得出做好預(yù)設(shè)，創(chuàng)設(shè)學(xué)生深度學(xué)習(xí)的機(jī)會(huì)。

2. 質(zhì)疑思辨，激發(fā)創(chuàng)新思維火花

情境2：投擲一枚質(zhì)地均勻的骰子，試驗(yàn)結(jié)果可否用數(shù)來(lái)表示？

分析：投擲的骰子可能會(huì)出現(xiàn)一點(diǎn)……六點(diǎn)，對(duì)應(yīng)數(shù)字為 1、2……6，此時(shí)，我們發(fā)現(xiàn)隨機(jī)試驗(yàn)的結(jié)果具有數(shù)字特點(diǎn)，這時(shí)我們可以用這些數(shù)字表示相應(yīng)的試驗(yàn)結(jié)果。如果拋一枚硬幣，結(jié)果為正面向上或反面向上，此時(shí)，結(jié)果不是數(shù)字，但我們可以分別利用數(shù)字0和1來(lái)表示 。

設(shè)計(jì)意圖：本情境設(shè)計(jì)是學(xué)生熟悉的擲骰子、拋硬幣游戲，為探尋隨機(jī)試驗(yàn)結(jié)果數(shù)量化路徑搭建了平臺(tái)，特別是為沒有數(shù)字特征的隨機(jī)試驗(yàn)結(jié)果數(shù)量化奠定了基礎(chǔ)。

3. 合作探究，凝練創(chuàng)新思維元素

問題1：通過(guò)情境1、情境2中的隨機(jī)變量與其概率的對(duì)應(yīng)關(guān)系，請(qǐng)給出離散型隨機(jī)變量及分布列的定義。

歸納：在這種對(duì)應(yīng)關(guān)系下，數(shù)字隨著隨機(jī)試驗(yàn)結(jié)果的變化而變化。像這種隨著隨機(jī)試驗(yàn)結(jié)果變化而變化的變量稱為隨機(jī)變量，常用字母[X]、[ξ]等表示 。所有取值可以一一列出的隨機(jī)變量稱為離散型隨機(jī)變量。

若離散型隨機(jī)變量[X]，可能取的不同值為[x1，x2，x3，]……[xn]，[X]取每一個(gè)值[xi]的概率[p（X=][xi]）[=][pi]，[i=1，2，3]……，[n]，以表格的形式表示如下：

上表稱為離散型隨機(jī)變量[X]的概率分布列，簡(jiǎn)稱為[X]的分布列。

設(shè)計(jì)意圖：既然分布列是特殊函數(shù)，那一定具備自己獨(dú)特的函數(shù)性質(zhì)，讓學(xué)生從函數(shù)研究角度對(duì)分布列性質(zhì)進(jìn)行探索，力求讓學(xué)生認(rèn)識(shí)到離散型隨機(jī)變量的概率分布列的內(nèi)涵，從而歸納出其性質(zhì)。

問題2：隨機(jī)變量和函數(shù)的概念有何異同？

請(qǐng)舉例進(jìn)行辨別。

設(shè)計(jì)意圖：通過(guò)對(duì)比隨機(jī)變量和函數(shù)，進(jìn)一步理解隨機(jī)變量的本質(zhì)，為后面通過(guò)函數(shù)思想解決概率問題奠定基礎(chǔ)。

4.展示提升，形成創(chuàng)新思維能力

情境3：在含有5件次品的100件產(chǎn)品中任意抽取4件，含有的次品件數(shù)[X]隨著抽取結(jié)果的變化而變化。問：

（1）[X]的取值范圍是什么？

（2）[X=0]、[X＜3]分別表示什么事件？

情境4：拋擲一枚質(zhì)地均勻的硬幣3次，請(qǐng)選擇合適的隨機(jī)變量<G:\2022年教學(xué)版配圖+四封\2022年12期教學(xué)\8-001.png>來(lái)表示實(shí)驗(yàn)結(jié)果？

設(shè)計(jì)意圖：通過(guò)利用隨機(jī)變量的語(yǔ)言描述來(lái)解決問題，體會(huì)隨機(jī)變量在表示隨機(jī)試驗(yàn)的結(jié)果上的簡(jiǎn)潔性和特殊性，體會(huì)如何選擇那些簡(jiǎn)單且有實(shí)際意義的隨機(jī)變量來(lái)表示隨機(jī)試驗(yàn)的結(jié)果，為后面隨機(jī)變量數(shù)字特征的研究奠定基礎(chǔ)。

問題3：在情境1中的方案2的抽獎(jiǎng)方案中，如果我們關(guān)心的是“顧客參加一次抽獎(jiǎng)活動(dòng)，是否中獎(jiǎng)”，該怎樣定義隨機(jī)變量[X]呢？請(qǐng)寫出這個(gè)隨機(jī)變量[X]取值的相應(yīng)概率。

分析：抽獎(jiǎng)結(jié)果為隨機(jī)變量[X]：設(shè)[X=]0[=]沒有中獎(jiǎng)， [X][=]1[=]中獎(jiǎng)。 則：

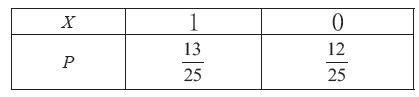
設(shè)計(jì)意圖：隨著對(duì)隨機(jī)現(xiàn)象的關(guān)注點(diǎn)不同，我們列出的隨機(jī)變量與其發(fā)生的概率的對(duì)應(yīng)關(guān)系也在變化。進(jìn)一步強(qiáng)化概率分布對(duì)于刻畫隨機(jī)現(xiàn)象的重要性，也借此滲透最簡(jiǎn)單的概率分布——二點(diǎn)分布，也可以用最簡(jiǎn)單的分布列為后面性質(zhì)的得出做預(yù)設(shè)。

問題4：觀察情境1中的方案2和問題3中的分布列，請(qǐng)給出離散型隨機(jī)變量分布列的性質(zhì)。

歸納：離散型分布列的性質(zhì)：

（1）[0≤Pi][≤1，i=1，2……n]。

（2）[P1+P2+P3+]……[+][Pn=1]。

5.反思悟道，培養(yǎng)創(chuàng)新思維品質(zhì)

問題5：為什么要學(xué)習(xí)隨機(jī)變量的概念？隨機(jī)變量的概念是通過(guò)怎樣的歷程得到的？它和我們熟悉的函數(shù)有什么聯(lián)系和區(qū)別？

問題6：社會(huì)實(shí)踐，以學(xué)習(xí)小組為單位，了解彩票“雙色球”“15選5”“大樂透”。（1）根據(jù)隨機(jī)變量的相關(guān)知識(shí)，定義它們各自的隨機(jī)變量[X]，并寫出其分布列。（2）利用電腦模擬預(yù)測(cè)其相應(yīng)的中獎(jiǎng)概率，并計(jì)算一張彩票的平均盈利情況。（3）通過(guò)本節(jié)課的學(xué)習(xí)和社會(huì)實(shí)踐，歸納總結(jié)出引入隨機(jī)變量分布列的作用。

設(shè)計(jì)意圖：?jiǎn)栴}5的設(shè)計(jì)，主要是讓學(xué)生真正意識(shí)到把隨機(jī)試驗(yàn)的結(jié)果數(shù)量化，用隨機(jī)變量表示隨機(jī)試驗(yàn)的結(jié)果，就可以更加深入地研究隨機(jī)現(xiàn)象，更能體現(xiàn)數(shù)學(xué)的工具性和應(yīng)用價(jià)值。問題6的設(shè)計(jì)讓學(xué)生在實(shí)踐中真正嘗試“三會(huì)”理念，為深度學(xué)習(xí)拓展了渠道，鞏固了創(chuàng)新思維品質(zhì)的培養(yǎng)。

三、反思與評(píng)價(jià)

1.注重?cái)?shù)學(xué)本質(zhì)探究，培養(yǎng)核心素養(yǎng)

本節(jié)課的設(shè)計(jì)立足于學(xué)生實(shí)際，通過(guò)問題串與系列情境發(fā)展了學(xué)生的思維能力，培養(yǎng)了學(xué)生的創(chuàng)新意識(shí)，增強(qiáng)了學(xué)生運(yùn)用數(shù)學(xué)知識(shí)解決實(shí)際問題的能力。無(wú)論是教學(xué)環(huán)節(jié)設(shè)計(jì)，還是數(shù)學(xué)情境創(chuàng)設(shè)，教師都要重視知識(shí)的產(chǎn)生過(guò)程，關(guān)注學(xué)生的長(zhǎng)遠(yuǎn)發(fā)展，注重學(xué)生的個(gè)體差異，結(jié)合分層教學(xué)，使不同的學(xué)生在數(shù)學(xué)學(xué)習(xí)上都能獲得進(jìn)步。

2.主導(dǎo)作用發(fā)揮充分，建構(gòu)深度學(xué)習(xí)

本節(jié)課通過(guò)生活中常見的具體實(shí)例（聯(lián)想與結(jié)構(gòu)），體會(huì)引入隨機(jī)變量的意義和價(jià)值，嘗試用數(shù)學(xué)的眼光看待生活問題。通過(guò)擲骰子和拋硬幣這兩個(gè)基本試驗(yàn)（活動(dòng)與體驗(yàn)），經(jīng)歷將隨機(jī)試驗(yàn)的結(jié)果數(shù)量化的歷程，通過(guò)6個(gè)問題的解決（本質(zhì)與變式），體會(huì)隨機(jī)變量引入的作用，嘗試用數(shù)學(xué)的思維分析生活問題。通過(guò)使用隨機(jī)變量的語(yǔ)言描述和解決問題（遷移與應(yīng)用），經(jīng)歷數(shù)學(xué)建模的過(guò)程，嘗試用數(shù)學(xué)的語(yǔ)言表達(dá)生活問題。通過(guò)反思所學(xué)內(nèi)容和情境問題的解決（價(jià)值與評(píng)價(jià)），提煉思想，發(fā)展數(shù)學(xué)核心素養(yǎng)。這五個(gè)環(huán)節(jié)的設(shè)計(jì)，讓學(xué)生親身經(jīng)歷了一次積極主動(dòng)的探索、歸納數(shù)學(xué)知識(shí)的過(guò)程，為學(xué)生的深度學(xué)習(xí)搭建了平臺(tái)，營(yíng)造了氛圍，創(chuàng)設(shè)了空間。

作者單位   陜西省西安惠安中學(xué)