《普通高中數學課程標準》中明確指出，高中數學課程要處理好數學學科核心素養與知識技能之間的關系，強調數學與生活以及其他學科的聯系，提升學生應用數學解決實際問題的能力，同時注重數學文化的滲透。以此為導向，近幾年的高考試題中融入了大量的以數學文化為背景的好題，不但考查學生的數學知識，而且有意識地培養學生的數學素養、道德情操，真正做到了全程育人、全方位育人。這些試題頻見于期刊，這里不再贅述。筆者主要收集了一些在高三教學中發現的好題，以饗讀者。

一、滲透數學文化，體現數學人文價值

1.數學文化滲透在立體幾何中

例1.（2020年東北師大附中二模）我國古代勞動人民在筑城、筑堤、挖溝、挖渠、建倉、建囤等工程中，積累了豐富的經驗，總結出了一套有關體積、容積計算的方法，這些方法以實際問題的形式被收入我國古代數學名著《九章算術》中。《九章算術·商功》中有：“斜解立方，得兩塹堵。斜解塹堵，其一為陽馬，一為鱉臑。陽馬居二，鱉臑居一，不易之率也。合兩鱉臑三而一，驗之以棊，其形露矣。” 下圖解釋了這段話中由一個長方體得到塹堵、陽馬、鱉臑的過程。已知塹堵的內切球半徑為1，則鱉臑的體積的最小值為______。

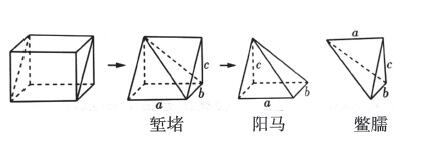
評析：我國古代有著非常輝煌的數學研究成果，涌現出了許多數學家和數學專著。《九章算術》是我國古代第一部數學專著，是《算經十書》中最重要的一部，其內容十分豐富：全書不但總結了戰國、秦、漢時期的數學成就，而且在數學史上首次闡述了負數及其加減運算法則。它的出現標志著我國古代數學形成了完整的知識體系。近幾年的高考卷中有很多試題都是從數學名著中選取素材，考查知識的同時，也讓學生了解中國燦爛的數學文化，培養學生的數學素養與情懷。

2.數學文化滲透在概率運算中

例2.（2020年山西太原模擬）七巧板是中國古代勞動人民發明的一種傳統智力玩具，由五塊等腰直角三角形、一塊正方形和一塊平行四邊形共七塊板組成。（清）陸以湉《冷廬雜識》卷一中寫道：“近又有七巧圖，其式五，其數七，其變化之式多至千余。體物肖形，隨手變幻，蓋游戲之具，足以排悶破寂，故世俗皆喜為之。”如圖是一個用七巧板拼成的正方形，若在此正方形中任取一點，則此點取自陰影部分的概率為______。

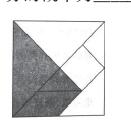
評析：七巧板游戲是大家喜聞樂見的，更是許多學生喜歡玩的智力游戲。該試題以七巧板為背景，考查幾何概型概率的計算。將這種蘊含著數學原理的智力游戲改編成試題，增強了考題的趣味性，也加深了學生對數學的重新認識：數學是好玩的！

3.數學文化滲透在導數運算中

例3.（2020年重慶八中月考）我們把分子、分母同時趨近于0的分式結構稱為[0/0]型。比如當[x→0]時，[ex-1/x]即為[0/0]型。兩個無窮小之比的極限可能存在，也可能不存在。因此，求這類極限時往往需要適當的變形，轉化為利用極限運算法則或重要極限的形式進行計算。洛必達法則是在一定條件下通過對分子、分母分別求導再求極限來確定未定式值的方法。如，

評析：該試題給出洛必達法則的內容和運算方法，讓學生快速理解并遷移到試題中，考查學生的讀題能力、數學理解能力以及對知識的遷移能力。這一類試題大都取材于一些高等數學知識，比如一些特殊的函數高斯函數、黎曼函數、狄利克雷函數等，一些獨特的數學概念泰勒級數、費馬數、阿波羅尼斯圓、皮克定理、凹凸函數等，一些特殊的數學思想極限理論、逼近思想、分割思想等。這些知識激發了學生的學習興趣，同時也讓學生對數學未知領域充滿了向往。

4.數學文化滲透于解析幾何中

例4.（2020年陜西銅川一中期末）圖1為陜西歷史博物館的藏品金筐寶鈿團花紋金杯，杯身曲線內斂，玲瓏嬌美。該杯形幾何體的主體部分可以近似看作雙曲線C:[x23]-[y29]=1的右支與直線[x=0,y=4,y=-2]所圍成的曲邊四邊形MABQ繞[y]軸旋轉一周得到的幾何體。如圖2所示，N、P分別為雙曲線C的漸近線與直線[y=4,y=-2]的交點，曲邊五邊形MNOPQ繞y軸旋轉一周得到的幾何體的體積可由祖暅原理（冪勢既同，則積不容異。意思是兩等高的幾何體，如果在同高處被截得的兩幾何體的截面面積均相等，那么這兩個幾何體的體積相等）求得，據此求得該金杯的容積是（杯壁厚度忽略不計）______ 。

評析：該試題是從歷史文物入手，提煉出解析幾何與立體幾何知識相融合的數學試題，具有一定的綜合性。前人為我們留下的一些經典音樂、繪畫、雕塑、建筑等藝術作品作為人類文化的瑰寶，具有非凡的魅力，也常常蘊含著深刻的數學內容、經典的數學方法，許多學者從中持續不斷地開發出一些新型的數學試題。這些試題提升了學生的審美情趣和藝術修養，同時也讓學生了解到數學是無處不在的，數學的應用是多元的，數學的魅力是無限的，數學是美的！

5.數學文化滲透于數列綜合應用中

例5.（2020年吉林第二次調研試題）牛頓（1643.1.4—1727.3.31），英國皇家學會會長，著名物理學家，同時在數學上也有許多杰出貢獻。牛頓用“作切線”的方法求函數f(x)的零點時給出一個數列[xn]：滿足[xn+1=xn-fxnfxn]，我們把該數列稱為牛頓數列。如果函數[f(x)=ax2+bx+c(a>0)]有兩個零點1、2，數列[xn]為牛頓數列，設[an=1nxn-2xn-1]，已知[a1=2],[xn>2,]則[an]的通項公式為______。

評析：該試題以偉大的物理學家牛頓命名的牛頓數列為試題背景，綜合考查函數與數列知識，具有一定的難度，同時也讓我們認識到牛頓不僅是一位杰出的物理學家，而且在數學領域也頗有建樹，是一位百科全書式的“天才”。

6.數學文化滲透于程序框圖應用中

例6.（2020年桂林調研考試）很多關于整數規律的猜想都通俗易懂，吸引了大量的數學家和數學愛好者，有些猜想已經被數學家證明，如“費馬大定理”，但大多數猜想還未被證明，如“哥德巴赫猜想”“角谷猜想”。“角谷猜想”的內容是：對于每一個正整數，如果它是奇數，就將它乘以3再加1；如果它是偶數，則將它除以2。如此循環，最終都能得到1。下圖為研究“角谷猜想”的一個程序框圖，若輸入n的值為10，則輸出的i的值_____。

評析：數學史上，長時期未能解決的數學猜想特別多，并且很多都是世界級的難題！這些猜想如同鑲嵌在數學皇冠上的明珠，千百年來吸引著眾多數學家為其不懈努力！本題以著名的“角谷猜想”為背景，讓學生了解“角谷猜想”的基本內容并進行簡單的應用，提升了學生的數學興趣和解決這些猜想的無限動力！

二、 結合時政新聞，體現數學德育功能

例7.（2020年陜西省高三二模）2019年底，武漢突發新冠肺炎疫情，2020年初開始擴散。黨中央、國務院面對“突發災難”果斷采取措施，舉國上下，萬眾一心支持武漢，全國各地醫療隊陸續增援湖北，紛紛投身疫情防控與救治病人之中。為了分擔“抗疫英雄”的后顧之憂，某校教師志愿者開展“愛心輔導”活動，為抗疫前線醫務工作者子女進行在線輔導。春節期間隨機安排甲、乙兩位志愿者為一位初中生輔導功課共3次，每位志愿者至少輔導1次，每一次只有1位志愿者輔導，則甲恰好輔導2次的概率為_____。

評析：這類試題往往以國家正在發生的時事新聞、新方針政策、公眾共同關注的熱點問題等為背景，甄選一個角度，抽象出數學模型，提煉出數學問題。既能達到一般試題的考查效果，也能達到育人的目的。這道試題解決起來并不難，學生可以很快地將題干部分轉化成熟悉的概率模型。似乎前面的“情境”無關緊要、可有可無，但正如前面所言“我們要借助一切機會進行全程育人、全方位育人，將我國眾志成城、萬眾一心、合力抗疫的英雄壯舉融入到數學試題中去，培育學生的大愛大德大情懷”！

筆者引用幾例以此說明數學文化越來越多地被我們數學工作者重視，正“潤物細無聲”地滲透到教學的各個環節中去！筆者也呼吁：讓我們攜起手來，共同挖掘數學文化，將其運用到教學中去，為培養新時代新人共同努力！

作者單位 陜西省西安市第七十中學 西安市慶安初級中學