一、以數助形

在北師大版初中數學教材中，學生需要學習的“形”，主要是平面圖形與幾何圖形。而“以數助形”就是將幾何問題代數化，利用數軸或者平面直角坐標系等方法解決幾何問題。

初中生可能對于“以數助形”的解題方法有所了解，但對于這個方法的運用還不是很熟練。其主要原因有兩點：一是對于圖形的基本性質掌握不熟練，以至于在做題時無法獲得題目中的隱藏信息；二是對此方法的運用較少，解題時不能馬上想到用“以數助形”的方法解決。那么既然找到了原因，我們就需要從根源上解決問題，幫助學生掌握簡單快捷的解題技巧，提高學習效率。在平時的教學中，數學老師需要幫助學生理解記憶圖形的特點和性質，對于與圖形相關的定理要牢牢掌握，幫助學生分析題目的隱藏條件，從而讓學生學會自己掌握；同時也要讓學生對這一解題方法進行大量練習，熟練掌握這一技巧，在做題時達到事半功倍的效果。在課堂教學中，老師也要注重學生“以數助形”能力的培養，促進學生對圖形的認識和理解。讓學生在解決問題時，形成多思考的習慣，促進學生思維能力的發展，幫助學生學好數學。

二、以形助數

數是學習數學的基礎，隨著學習的不斷深入，學生接觸到的數越來越多，難度也越來越大，在解決有關“數”的問題時，經常會因為馬虎大意，出現計算錯誤。而運用“以形助數”的解題方法，能夠將幾何圖形直觀清晰的優勢發揮出來，提高解題效率。在北師大版數學教材中，“以形助數”的解題技巧可以幫助學生用幾何圖形來理解記憶一些代數的公式。

例如，完全平方和公式，它的定義是兩個數和的平方，等于它們的平方和，加上它們的積的2倍。如果讓學生死記這個公式，學生可能能夠記住，但是有些學生可能理解不了公式的意義，以至于不能很好利用。這時我們可以用“以形助數”的方法，利用幾何圖形給學生講解完全平方和公式。也就是取線段a和線段b，作出a+b，并以a+b為邊長，畫一個正方形，并作ab連接點平行于正方形的線段（如圖），從這個直觀的圖形上學生就可以理解完全平方和公式的定義了。

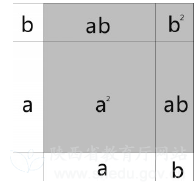
“以形助數”的技巧還可以幫助解決一元二次方程和平面直角坐標系的問題，把代數的表達式賦予幾何意義，從而幫助學生簡化代數運算，解決相關的代數問題。當然并不是所有的代數問題都能夠轉化成幾何問題來解決，因此，教師在教學中也要訓練學生理解題意，判斷題目能否轉化，讓學生多思考，多分析題意，促使問題有效解決，提高解題效率。

三、數形結合

數形結合對于初中學生二元一次方程和一次函數的學習有很大幫助，能夠使學生在遇到這種題目時，多思考，多轉化。

例如，北師大版八年級教材中的例題，甲、乙兩地相距100千米，A、B兩人同時分別從甲、乙兩地騎車相向面行，假設他們都保持勻速行駛，則他們各自到甲地的距離s(km)都是騎車時間t(h)的一次函數，1小時后B距離甲地80km，2小時后A距離甲地30km，兩人需要多久相遇？對于這樣的題，老師可以在分析題目的同時，引導學生將坐標圖畫出來，通過坐標圖，我們可以直觀地看到題目內容，但為了確保答案的準確性，同時也需要使用代數的方法，通過列方程來解答問題。這就是將平面幾何與代數相結合的實例，作為數學教師，我們可以在平常的教學過程中，多培養學生對于數形結合方法的使用，首先需要讓學生對于基礎的概念、性質掌握牢固，再讓學生學會分析題目的潛在條件，讓學生多思考，靈活運用數形結合的解題方法。

總之，數形結合思想能夠促進學生空間觀念的培養，能夠使復雜的數學問題簡單化、具體化。培養學生數形結合的思想，不僅是老師的教學要求，還是學生學習數學的必備能力，它能夠促進學生思維能力的發展，提高課堂效率，讓學生學好數學。

作者單位 山東省青島市城陽第十一中學