一、四年級解決問題教材分析

（一）內容斷層

從整體上來看，三年級有關解決問題教學的內容很多，同時它的定位也比較清晰，有歸一問題、歸總問題，連乘或連除等。這些模型的教學，可以幫助學生更好地理解與遷移，也有利于教師教學。但四年級的解決問題教學，只有兩個常用的模型，運用單價、數量和總價以及速度、時間和路程，而且計算也都只需一步。五年級的解決問題教學，以方程的解決問題教學為主，而方程的主要結構，也以兩積之和ax+bx=c的結構為主。

斷層一：解決問題難度，提升不明顯

三年級的解決問題以兩步計算為主，比如三年級上冊的歸一、歸總問題，三年級下冊的連乘與連除問題等。但到了四年級的解決問題例題，只有簡單一步關系的運用，比如單價、數量和總價或者速度、路程和時間等，缺少復雜問題的練習。而到了五年級，學生對于方程問題又需要三步計算，因此四年級對于解決問題的編排，不管是習題類型，還是解決難度，都有一定的斷層，沒有給學生合適的基礎來適應五年級解決問題。

斷層二：解決問題模型，沒有相應支持

五年級的幾個方程常用模型，都需要建立在兩積之和的基礎之上，但四年級解決問題的教材中，并沒有兩積之和的專題解決問題的教學。反而在各單元零散會出現一些習題。這樣的習題教學，肯定不利于學生去提煉和學習，學生如果對這種結構不熟練，肯定會影響其后續兩積之和方程的學習。

（二）分布零散

仔細分析四年級數學解決問題的一些習題，發現兩冊教材中也有一些零散的兩積之和結構的例題或習題。但由于習題分散，而且不同的單元都有自己的教學任務，不利于學生去提煉和感悟兩積之和的結構。

比如，人教版四年級教材第四單元《三位數乘兩位數》P50。

學校要為圖書館增添兩種新書，每種買3套。一共要花多少錢？

在該習題中，雖然有著兩積之和的模型，但由于教材是需要各買3套，教師比較容易會把解決問題的重點放在運算定律的討論，而弱化了其中兩積之和的結構。而且僅有一道習題的練習，肯定不利于學生整體感悟結構。

二、有效的策略

面對以上這些現象，筆者認為教師一定要善于整合教材，基于數形結合，多角度、多形式來幫助學生跨越斷層，建構模型，從而幫助學生不斷提升解決問題的能力，為五六年級的數學解決問題學習打下扎實基礎。

（一）化零為整，跨越斷層

化零為整，跨越斷層，主要是教師要整體呈現結構相同的習題，通過比一比，解一解，編一編等多種形式來幫助學生掌握解決問題的方法，提升解決問題的能力。

1.化散為整，整體呈現

在四年級人教版教材或其他練習中，有著大量結構相同的習題，其中也有兩積之和的習題。化散為整需要教師精心選擇習題，并把結構相似的習題進行整體呈現，引導學生在解答、比較與歸納中感悟兩積之和的模型。

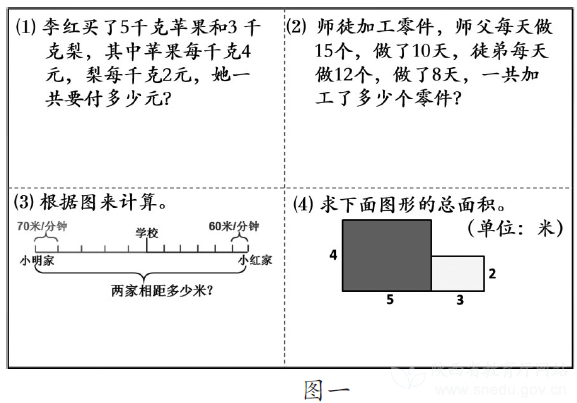
例如，上面的四道習題（如圖一），來源于配套習題，并適當進行了修改。這些習題都需要利用兩積之和的結構來解決問題。通過讓學生集中練習，有利于學生提煉與感悟模型。

2.化解為變，整體改編

學生解決問題能力的提升需要建立在大量的習題練習之上，但數學學習的時間非常有限，因此有效提升解決問題的能力，就需要把一類題型或一種題型練得更透。“化解為變”就是以其中一道題目為素材，通過條件或問題的不斷變化，在變與不變中展開練習，從而提升解決問題的能力。

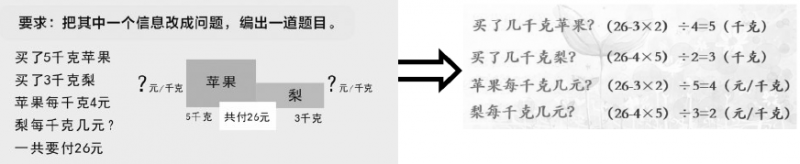
例如，在上題中，當我們解決了一題習題后，要求學生把其中一個信息改成問題，編出一道題目。學生通過編一編，算一算，由于計算不成問題，學生可以較快解決所有問題。因而就給了學生更多練習的機會，提升了解決問題的能力。

3.化變為聯，整體遷移

建構主義理論認為：知識的學習需要建立在學習者已有經驗的基礎之上，因此，教師需要不斷幫助學生把新知與舊知結合起來，形成新的知識鏈。而化變為聯就是幫助學生在不斷變化中聯系舊知，從而幫助學生更好地融合知識，提升解決問題的能力。

通過變式，教師引出了上題（如圖），其中最大的變化就是去掉了兩種水果的數量，改成了兩種水果的數量之和。這樣的變式主要是為了幫助學生感受到兩積之和的問題與雞兔同籠問題之間的聯系，從而幫助學生深入感悟模型，提升解決問題的能力。

（二）數形結合，構建模型

數學模型的建立需要經歷多個階段，筆者認為一般需要經歷初步感悟、提煉模型、深入感悟、運用模型等環節。在這些環節中，數形結合使學生從模糊到清晰，從陌生到熟練，從學習到遷移。借助數形結合，可以更好地幫助學生構建模型，提升解決問題的效率。

1.情境創設融入數與形，初步感悟

在情境創設引入新課時，設計數形結合的習題，不僅可以調動學生的學習興趣，同時也為學生初步建立數與形之間的聯系埋下伏筆。學生借助圖的直觀，可以初步感悟兩積之和模型。

例如，圖一的四道習題，教師就呈現了不同類型的習題，其中就有純文字和純圖形的習題。這樣數形結合的情境，可以讓學生更好地開展對比與交流，可以幫助學生更好地初步感悟模型。

2.思維關鍵求聯數與形，提煉模型

數學模型的提煉需要學生不斷通過比較，在不同的情境中尋找相同的關系。借助圖形的直觀，教師需要引導學生去溝通形與數之間的關系，從而使學生發現數中的關系與形的數量是一樣的，都是利用相同的結構，從而逐漸提煉兩積之和的模型。

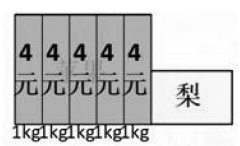
例如，在上題的情境中（如上圖），當讓學生來尋找習題的相同點時，大多數學生都會先找到數與形之間的聯系，既大長方形的面積等于蘋果的總價，小長方形的面積等于梨的總價。教師還可以追問：“明明是面積，為什么會等于總價呢？”通過引導學生思考與比較，學生就會發現大長方形的長和寬與蘋果的單價和數量之間的聯系，從而幫助學生深入理解兩積之和結構。

3.思路變化凸顯數與形，深入感悟

為了讓學生更好地理解模型，運用模型，教師還需要不斷變式習題，從變與不變中去幫助學生深入感悟模型。而借助數與形的變式，則可以更直觀呈現不同變式下的相同點，幫助學生深刻理解模型。

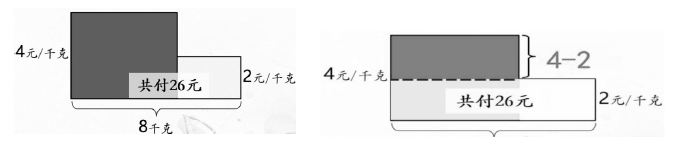
例如，在兩積之和的最后環節（如上圖），我們設計了變式練習，把習題改成了“李紅買蘋果和梨共付26元，蘋果每千克4元，梨每千克2元，兩種水果共買了8千克。買了幾千克蘋果和幾千克梨？”為了幫助學生理解，可以把8千克全部看成2元，上面黑色的長方形就是10元，利用10元去除以兩種水果的單價，就可以算出大長方形的長是5千克，那么剩下的小長方形的寬就是3千克。這樣直觀呈現假設的圖形，可以幫助學生理解其中的方法，突破難點。

關注習題的研究，教師需要更深入了解習題練習的目的，不斷通過整合、對比、建模等幫助學生深入學習解決問題，感悟其中的本質，提升解決問題的能力。相信，通過不斷研究一定能較好地促進學生解決問題能力的發展。

作者單位 浙江省杭州市蕭山區漁浦小學 浙江省杭州市濱文小學