解題時可以這樣想：695比700少一些，接近700；703比700多一些，也接近700。所以，695≈700，703≈700。

這里，不談近似數，也不談“四舍五入”，這些在四年級下學期學生認識了“萬級、億級的多位數”時再研究。這里，更多的是幫助學生對數量的一個直觀的感悟。

但是，在接下來的練習中，學生做到諸如這樣的題目，卻會發生錯誤：3091≈4000。某班有48人，其中13人發生了這樣的錯誤，究其原因，因為看到了“91”，就誤認為接近“4000”了。所以，雖不去明確“四舍五入”的概念，但對“接近數”的區域的劃分，還是應該幫助學生明確。

課中，我和學生一起進行了下面的嘗試：

一、點數結合，明確“接近數”的區域

出示：

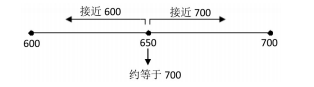
師：在600和700之間，還有哪些數？

學生想出了比如620、635、650、677這些數，繼而發現從601、602、603一直到699都在其中。

師：在這些數中，一些數接近600，一些數接近700，你能把這些數分別找出來嗎？

雖然這些數沒有一一標在線段上，但借助于直觀的線段，無形的點與相對應的數結合，學生會發現要把這些數一分為二，650左邊的部分接近600，650右邊的部分接近700。那650離600和700一樣近，它怎么辦呢？在這里，明確指出：雖然650離600和700一樣近，但一般情況下將它約等于700。

二、看數想點，在區域中正確找“接近數”

明確了找“接近數”的區域，這時，再領著學生回到書中習題的解決中，思路會明朗化很多。

看一個數是接近幾百還是幾千，學生不再僅僅是建立在直觀感知上，而是將這個數放到一個區域中去，找到這個數在這個區域中的位置再進行判斷。比如，判斷695接近幾百，2399接近幾千，學生可以這樣分析：

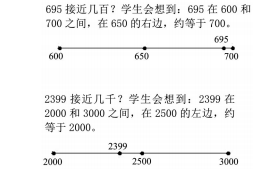
這一系列的思考，對學生來說也是一種挑戰。比如，695在600至700這個區域的什么位置？在600至700之間的數，會像彈珠一樣一個接一個地從學生頭腦中蹦出來，這些數被正中間的“650”給分在了兩邊，要找到695所在的位置，學生還會下意識地再分，分成610、620、630這樣的小段，那么，695就在690和700之間。這個思考過程，其實也可以幫助學生強化對數的順序的鞏固認識。同時，找“接近數”，學生強烈地感受到“中間數”的重要性。

三、卡片擺數，在“是否”中感受分界點

用四張數字卡片，可以擺出多個不同的四位數，這些四位數分別接近幾千？學生可以在相應區域中找數的位置進行判斷。而反過來，給出一個接近的整千數，按要求來擺數，就要逆向思考，且更具理性。

比如，用0、1、4、7擺一個接近2000的四位數，可以怎樣擺？

首先，要考慮千位上怎么擺。擺出的數要接近2000，所以，這里千位上只能擺數字1。接下來，百位上可以擺幾？這就需要深入思考。所擺的四位數在1000至2000之間，而且在1500的右邊，所以，百位上可以擺7，但不可以擺4和0。這里，百位上擺數字幾，可謂是重中之重。這就為“一個數最高位是千位，求這個數接近于幾千，要看百位數”埋下伏筆。

所以，在低年級教學研究中，我們既要遵循學生直觀思維的認知規律，同時，通過一定的方式，努力引導他們的思維往深處、往寬處去走一走，幫他們架起一座通往思維深層次的橋梁。

作者單位 江蘇省南通師范第一附屬小學