題目：如圖，在△ABC中，CH是外角∠ACD的平分線，AB=AC。則∠A等于多少度時，AB∥HC ?

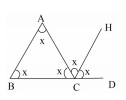
師：對這種探究條件使得某個結論成立的問題，我們通常假設結論成立，然后由此結論逆推所需條件，于是假設AB∥HC，得到什么結論？生：∠A=∠ACH。生：∠B=∠HCD。

師：∠A=∠ACH有什么依據？生：兩直線平行，內錯角相等。

師：∠B=∠HCD有什么依據？生：兩直線平行，同位角相等。

師：通常求角度的問題，我們一般會怎樣處理？生：設未知數 x 。

師：那么我們設∠A=[x]，于是哪些角就可以表示出來？生：∠ACH=x。

師：題目中還有什么條件？生：AB=AC。生：CH是外角∠ACD的平分線。

師：AB=AC這個條件怎么用？生：可以得到∠B=∠ACB。

師：CH是外角∠ACD的平分線，這個條件怎么用？生：可以得到∠ACH=∠HCD。

師：得到這些結論后，還有哪些角可以用[x]表示？生：∠ACH=x， ∠B=∠ACB=x。（學生說，老師在圖形上標記。）

師：我們設了未知數，表示完相關角之后，接下來應該怎么做呢？生：……（大部分學生在思考，個別學生不確定地、試探地回答說需要列方程。)

師：設未知數必然要列方程，只有通過列方程、解方程才能求得未知數的值。方程思想是數學中非常重要的思想。 那么列出的方程是什么？生：3x=180°。最終解得x=60°，所以∠A=60°。

師：下面我們把分析過程轉化成解題過程。解題過程有兩種方式， 第一種方式：假設AB∥HC ，再以此為條件寫解題過程，即把剛才的分析過程順次寫下來，補充上理由即可；第二種方式：經過分析我們得到∠A=60°，于是我們以∠A=60°為條件，推理出AB∥HC。同學們思考一下，可不可以這樣做？你們有什么疑問？生：老師我們不是剛才分析∠A=60°是結論嗎？怎么又成了條件了？

師：這個問題提得特別好！我們回到題目中去，題目要求是∠A等于多少度時，AB∥HC？相當于問∠A滿足什么條件時，AB∥HC？經過我們剛才的分析，得到∠A=60°，于是∠A=60°就是AB∥HC的條件，我們分析的結論恰恰就是AB∥HC的條件。

板書解題過程：∵ AB=AC ∴ ∠B=∠ACB

師：接下來 ∵ ……（學生茫然不知該回答什么，改變問法。）

師：又 ∵ ∠A=60°。 生：∴ ∠B=∠ACB=60°。

師：可以繼續得出什么結論？（學生茫然不知該回答什么，改變問法。）

師：∠ACD等于多少度？生：∠ACD=120°。

師：∵ …… （學生茫然不知該回答什么，改變問法。）

師：∵ CH是外角∠ACD的平分線。生：∴ ∠ACH=∠HCD。(角平分線定義)

師：可以繼續得出什么結論？（學生茫然不知該回答什么，改變問法。）

師：∠ACH=∠HCD等于多少度？生：∠ACH=∠HCD=60°。

師：可以繼續得出什么結論？（學生茫然不知該回答什么，改變問法。）

師：∠A與∠ACH有什么數量關系？生：∠A=∠ACH。

師：能否得到AB∥HC？生：能！內錯角相等，兩直線平行。（學生回答得很響亮）

在這堂課教學過程中，從學生對老師第一種提問方式茫然無措到老師改變問法后順利回答，可以看出學生根本不知道老師要把他們引領到哪里。這種教學對學生來說其實毫無效果！因為學生始終處于盲目狀態。這就如同牽引一個被蒙住眼睛的人走路，你給他一個指令他走一步，在一個個指令下他一步步走向終點，每一步似乎都是他在走，但他始終不清楚方向，因此當他脫離指引后就茫然不知所措了。所以，分析問題時要時刻提醒學生樹立問題意識，不要忘了目的是什么，要解決什么問題。為此，我總結出了這樣一個分析問題的流程：牢記所要解決的問題，即明確目標purpose或明確去哪里（where）——解決這個問題需要滿足什么條件what）——尋求滿足該條件的條件（look for）（從已知或圖形中尋找）——寫出由已知或圖形所得到的結論——篩選出能夠解決本問題的結論——提煉整理解題過程。在每一次的教學過程中不斷提醒學生這樣做，鼓勵學生大膽質疑，在聽課時多問幾個“準備到哪里去？為什么要到那里？”這些問題搞明白了，學生就弄清楚了整個分析思路，才真正地聽懂了，并逐漸從中體悟到分析問題的方法，提高自己分析問題的能力，從根本上解決“上課聽懂下課不會做”這個問題。

作者單位 陜西省西安市第六中學