幾何直觀主要是指利用圖形描述或者分析問題。幾何直觀在小學數學的應用范圍很廣，探尋幾何直觀的教學價值可以對學生的數學學習起到明顯的促進和推動作用。在實際教學中，如能根據教學需要靈活運用，將會起到意想不到的效果。

一、借助幾何直觀，幫助學生理解算理

幾何直觀對于促進學生對數學內容的理解起到了推動作用。尤其是在分數乘除法的教學中，一些算理的理解相較于其他數學運算來說要顯得復雜而抽象許多，教師如果能夠借助幾何直觀來引領學生學習的話，那么，學生對算理的理解也就會顯得更加輕松。

如在教學《分數乘法》這部分內容的時候，以[1/2]×[1/4]為例，筆者是這樣引領學生進行教學的：同學們，看到這個算式，你有什么想法？有學生說這個算式就是指把[1/2]平均分成4份，求其中的一份是多少。在學生回答完畢以后，教師又繼續追問道：你能用畫圖來表示嗎？

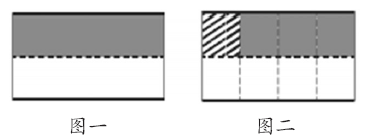
在學生畫出圖以后，我又讓學生把自己的理由說一說。學生說在這個圖中，圖一黑色區域表示的是[1/2]，圖二中畫斜線的小方格區域就是指[1/2]的[1/4]是多少，它的結果也就是[1/8]，也就是說[1/2]的[1/4]占總單位1的[1/8]，如此教學，直觀清楚，學生們對算法算理的認識也更加深刻。

二、借助幾何直觀，幫助學生建立表象

在學生數學學習過程中，有些數學知識，學生們雖然經歷了探索過程，但是，由于數學知識結構本身的復雜性，學生在理解和運用上還是具有一定困難的，如果學生們不能攻克這個數學難題，會給學生的學習造成一定障礙，在這種教學情形下，教師可以借助幾何直觀幫助學生建立數學表象，以降低學生的學習難度，提升學習效果。

如在教學《乘法分配律》這部分內容的時候，乘法分配律與其他運算律相比較來說，結構相對復雜，學生在運算的時候很容易出現各種錯誤，因此在教學這部分內容的時候，教師除了讓學生感受到乘法分配律的意義之外，如能借助幾何直觀幫助學生在頭腦中建立起乘法分配律的表象，那么，學生對所學知識的印象會更加深刻。為了幫助學生建構乘法分配律的表象，我主要以下面的例子展開了教學：有一塊長方形地，一邊種的是蘿卜，長是a米，一邊種的是白菜，長是b米，請問這塊菜地一共有多少平方米？（如右圖）

學生們借助幾何直觀很快得出了a×c+b×c以及（a+b）×c兩種算法，這樣一來，學生借助圖形找出了它們與乘法分配律之間的聯系。與此同時，學生們對于乘法分配律的變式也有了更進一步的感受與體會，學習效果顯著。

三、借助幾何直觀，幫助學生展開推理

皮亞杰在認知發展階段論中指出：具體運算階段的兒童雖然不能進行抽象的邏輯推理，但是，可以憑借具體形象進行直觀推理。基于此，在解決一些數學問題的時候，教師就可以借助幾何直觀的特點，幫助學生展開數學推理，以提升數學學習效果。

如在教學《分數的大小比較》這部分內容的時候，在[1/6]與[1/5]兩個分數的大小比較上，有學生采用整數遷移的辦法，認為：因為6大于5，所以[1/6]大于[1/5]，怎樣才能幫助學生改變錯誤的思想認識呢？教師可以借助幾何直觀的教學策略來解決，于是，我讓學生準備兩個大小一樣的圓先分一分，再涂一涂。

（如右圖）

然后再讓學生在圓圈里填上合適的數，如此一來，借助直觀的圖片，學生們可以清楚地對兩個分數的大小進行比較。與此同時，借助幾何直觀也可以使學生的推理能力得到有效培養與發展。

總之，幾何直觀作為數學新課標的核心詞語之一，教師要對其充分重視，并且能夠極力挖掘教材中可供學生用圖形描述或者分析的具體問題，從而使幾何直觀的教學價值落到實處。