蘇霍姆林斯基說過：“教育的技巧并不在于能預見到課堂的所有細節(jié)，而是在于根據(jù)當時的具體情況，巧妙地在學生不知不覺中做出相應的變動。”從課堂的視角來看，這里所說的“當時的具體情況”就包括了生成。

生成是課堂上必然出現(xiàn)的情形，是學生利用自己的經(jīng)驗與教師所提出的問題或講授的知識點進行碰撞的產(chǎn)物。課堂上的生成，既是學生已有思維的體現(xiàn)，也是引導課堂走向新的境界的契機。在精心進行課堂設計的基礎上，教師要充分運用自己的教學智慧在不斷變化的課堂上發(fā)現(xiàn)、判斷、整合信息，根據(jù)師生交往互動的具體進程來整合課前的各種預設。通過教師與學生分享彼此的思考、經(jīng)驗和知識，交流彼此的情感、體驗與觀念，從而求得新的發(fā)現(xiàn)，使課堂煥發(fā)出生命活力，創(chuàng)造出發(fā)展的、生成的課堂。

在一節(jié)數(shù)學活動課中，我們遇到了這樣一道練習題：右圖是用1∶500的比例尺畫出的圖形。你能計算出它的實際面積嗎？

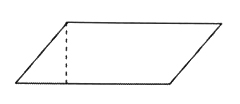
我剛把題目展現(xiàn)出來，學生們就紛紛舉起了手。我心里暗自得意：看來學生對比例尺的知識都掌握得不錯，心里有說不出的成就感，我就指名學生回答解題思路。“要想知道圖形的實際面積需要先量出平行四邊形的底和高，然后根據(jù)平行四邊形的面積公式用底乘以高求出它的面積，再除以比例尺就可以得出它的實際面積了。”我沒有立即對這個同學的回答進行評價，而是接著問了一句：“能說出這樣解答的道理嗎？”我這一問好像是多余的，把好多學生都問愣住了。正當學生們無從回答時，坐在教室東北角的王唯一舉起了手。他回答道：“我認為應該先測量出平行四邊形的底和高以后，根據(jù)比例尺先算出平行四邊形實際的底和高，然后再用底乘以高求出它的實際面積。”這時課堂上傳出了學生們的議論聲，王唯一的回答無疑讓學生們的思維產(chǎn)生了漣漪。此時，學生們都瞪著眼睛要聽我的結論。我卻讓這兩個學生按各自的思路到黑板上進行了演示：

兩種思路的結果為什么會差別如此之大呢？問題出在哪里？一石激起千層浪，學生們又陷入了沉思之中。經(jīng)過小組討論交流后，部分學生高高舉起了手。我還是把給同學們解答疑惑的機會再次交給了王唯一。“比例尺是圖上距離和實際距離的比，它應該指長度單位之間的關系，而不是指面積單位之間的關系，比例尺表示的是平行四邊形圖上距離和實際距離的關系，不是圖上面積和實際面積之間的關系。如果我們先算出平行四邊形的圖上面積，再求實際面積，結果就有區(qū)別了。”經(jīng)他這樣一說，學生們恍然大悟，并向他投去了信服的目光，我也為他豎起了大拇指。伴隨著下課鈴聲響起，學生們帶著滿意的笑容結束了這節(jié)課的學習。

反思：數(shù)學教學是數(shù)學活動的教學，是師生之間、學生之間交往互動與共同發(fā)展的過程。在實施教學的過程中，教師應直面真實的教學，根據(jù)師生交往互動的具體進程來整合課前的各種預設,讓學生充分發(fā)表自己的獨立見解，才能使課堂綻放生命活力，真正使預設與生成共精彩。在以上的教學中，當學生思維出現(xiàn)偏差時，教師沒有把正確的結論告訴學生，而是利用學生概念模糊不清這一錯誤，及時改變了課前的預設方案，運用問題引領的方式，為學生創(chuàng)設充分的思考時間和交流空間，“能說出這樣解答的道理嗎”“兩種思路的結果為什么會有天壤之別呢？問題出在哪里？”“逼”著學生在頭腦中再次對所學知識進行有序的思考和梳理，找出所學知識和實際應用之間的橋梁，使問題得以圓滿解決。

進一步反思課堂上的生成，筆者還有這樣的幾點認識：課堂上只有尊重學生的想法，生成才有可能出現(xiàn)；課堂上要給學生大膽表達的機會；學生必須有充分思考的機會，要善于將教師所教的內(nèi)容或者所提出的問題與自己的已有知識聯(lián)系起來，這樣生成才有成長的土壤。一個重要的策略就是，教師在課堂上要讓學生的思維活躍起來，教師要鼓勵學生大膽地聯(lián)系、大膽地想象，還要讓學生善于將自己的思考變成大家都聽得懂的語言，這樣教師在加工生成的時候，才會更有意義。

總的來說，讓學生在反思、交流的過程中理清了概念的本質(zhì)。學生不僅明確了錯的原因，而且起到了觸類旁通的效果，在以后的練習當中也證明了這一點。教師改變了一個預設，學生還了一個精彩課堂。