【原題呈現(xiàn)】

人教版小學(xué)數(shù)學(xué)一年級下冊第7頁的練習(xí)題第8題是這樣的（如圖1）：

題目不問別的數(shù)字的對面數(shù)，只問“4”的對面數(shù)，估計編者的意圖是讓學(xué)生動手后用排除法來說明“4”的對面不可能是“1”“2”“5”“6”，只能是“3”。但是，根據(jù)本人的教學(xué)實踐，編者的意圖有點“一廂情愿”的味道：不說一年級的學(xué)生，就算二三年級的學(xué)生，能這樣說理的學(xué)生也不多。

我覺得，解決這個問題最好的辦法就是“手腦”結(jié)合，讓學(xué)生先動動手，畫一畫，剪一剪，折一折，再看一看，想一想，說一說，總結(jié)規(guī)律，并利用規(guī)律進(jìn)行思考。

【教學(xué)描述】

一、猜一猜

在動手折之前讓學(xué)生看著圖畫靜靜地思考1分鐘左右，并猜一猜“4”的對面是幾？并說說理由。首先，個別空間觀念強(qiáng)的學(xué)生可能會猜出來并說出理由。其次，讓學(xué)生在動手之前先觀察圖形，展開合理的想象，再進(jìn)行問題思考。

二、剪一剪

先讓學(xué)生畫在紙上，然后用剪刀剪下來，折一折。這件事情看似簡單，但對于一年級的小朋友來說卻是困難重重。第1個難點：畫不好；第2個難點：折不清楚；第3個難點：不理解“對面”的概念。因此，更需要給孩子動手的機(jī)會。

三、想一想

動手之后大部分學(xué)生知道了答案，卻不知道為什么“4”的對面是“3”。因此，在動手操作完成后必須馬上追問一句：“哎！為什么“4”的對面是“3”而不是其他數(shù)呢？”讓學(xué)生去追尋表象背后的原因，有利于培養(yǎng)學(xué)生“知其然，更知其所以然”的良好思考習(xí)慣。

四、換一換

思考了背后的原理，還不代表會用原理解決問題。這時候，老師可以把圖形中的6個數(shù)字進(jìn)行調(diào)換，讓學(xué)生再來說一說調(diào)換后的圖“誰的對面是誰”，并說說道理，以此來鞏固根據(jù)位置來判斷對面數(shù)字的方法。

【實踐反思】

一、百“說”不如一“做”，“指尖”上才能出智慧

“人生兩個寶，雙手與大腦。動腦不動手，快要被打倒。動手不動腦，飯也吃不飽。手腦都會用，才算是開天辟地的大好佬。”陶行知這首膾炙人口的《手腦相長歌》，道出了手和腦統(tǒng)一的重要性。動手操作，是小學(xué)階段學(xué)生非常重要的一種數(shù)學(xué)學(xué)習(xí)技能訓(xùn)練手段。當(dāng)然，這是需要花時間的，而且還需要老師的悉心指導(dǎo)，但是這種在數(shù)學(xué)上花的時間比起更多無謂的講解應(yīng)該是非常有價值的，它可以培養(yǎng)學(xué)生的動手能力、觀察能力、思考能力、主動解決問題的能力。

二、操作前的“想象”是培養(yǎng)學(xué)生“空間觀念”的良好時機(jī)

操作前的“想象”是培養(yǎng)學(xué)生“空間觀念”的良好時機(jī)。這是非常重要的一環(huán)，但是，由于教學(xué)時間所限及個別教師教學(xué)理念的不到位，也是很容易被我們忽視的一環(huán):一上來就急匆匆地讓學(xué)生動手操作，看似十分重視“動手”能力的培養(yǎng)，實則不明白動手前的觀察和想象對學(xué)生的空間觀念的培養(yǎng)有多么重要。

三、操作后的“追問”可培養(yǎng)學(xué)生“數(shù)學(xué)思考”的良好習(xí)慣

百說不如一做，并不是說老師就不用說了。老師的說是必須的，而且還得說得巧，說得準(zhǔn)。如當(dāng)學(xué)生剪過折好，老師讓他找“4”的對面是幾的時候，學(xué)生能說出“3”當(dāng)然是不難的，關(guān)鍵是學(xué)生有沒有明白在這里為什么“4”的對面不是“1”，不是“2”，也不是“5”和“6”，只能是“3”？原因就是“4”與“1”“2”“5”“6”都是相鄰的，不可能相對，所以只能是“3”。但是，這樣還不夠，因為這種方法還不能幫助學(xué)生解決別的數(shù)字的對面是幾的問題，必須要讓學(xué)生找到最佳策略：尋找這個數(shù)字隔一格的數(shù)字。

當(dāng)學(xué)生會找?guī)椎膶γ媸菐椎臅r候，在時間允許的情況下，我們還可以繼續(xù)深入，把6個不同的數(shù)字換成6種不同的顏色（對于一年級的小朋友來說，顏色絕對比數(shù)字更有吸引力）。讓學(xué)生猜猜折成正方體后哪兩種顏色是相對的，不是更有趣味和數(shù)學(xué)味嗎？

如果還想更深入一些，也是可以的。告訴學(xué)生一個正方體中2和4相對，3和6相對，1和5相對，讓學(xué)生根據(jù)已知信息把展開圖的數(shù)字填出來。當(dāng)然，這個問題的答案是開放的，大約有20多種，如圖2：

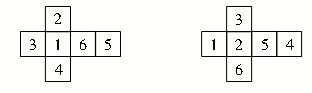
只要符合要求的答案都可以，開放型的答案更使題目具有數(shù)學(xué)味和人情味。