【例1】某電子廠加工一批電子零件，原計劃每小時加工120個，實際每小時加工了150個，結果比原計劃提前5小時完成，這批電子零件共有多少個？

常規法：先求出工作效率差：150-120=30（個），然后求實際工作總量是150×5=750個，則原來需要的時間是750÷30=25（小時），最后就可以求出這批電子零件的總個數是120×25=3000（個）。

倒數法：由于原計劃每小時加工120個，所以原計劃加工1個零件需要用[1120]小時；實際每小時加工了150個，則實際加工1個零件需要[1150]小時。因此，加工1個零件，實際用的時間要比原計劃少（[1120]-[1150]）小時，故此題可順利得解：5÷（[1120]-[1150]）=3000（個）。

評注：此題中的常規法需要先求出工作效率差和實際工作總量，然后在此基礎求出原來工作時間，最后才能求出原來工作總量，這一解題過程步驟過多，而倒數法思路簡單，清晰明朗，解答快捷。

【例2】甲乙兩地相距640米，小明和小紅同時從甲地出發去乙地，已知小明每分鐘走64米，走完全程小紅所用時間比小明少20%，小紅每分鐘走多少米？

常規法：因甲、乙兩地相距640米，小明每分鐘走64米，故走完全程小明需要640÷64=10（分鐘）；又因走完全程小紅所用的時間比小明少20%，故小紅需要10×（1-20%）=8（分鐘）。由此可知，小紅每分鐘走了640÷8=80（米）。

倒數法：將甲乙兩地之間的路程看作單位“1”，那么速度和時間互為倒數。因為走完全程小紅所用的時間比小明少20%，即小紅所用的時間是小明所用時間的（1-20%），所以小紅的速度是小明的[11-20%]。由小明每分鐘走64米，可以求出小紅每分鐘走64×[11-20%]=80（米）。

評注：當路程為“1”時，速度和時間互為倒數，此時巧妙地運用倒數轉換數量關系，往往可以使思路清晰，簡化解題步驟，收到意想不到的效果。

【例3】某公路建設隊在修2000米的運材路后，因增加了汽車，繼續修2000米只用了原時間的20%，少用了16小時，效率比原來增加了百分之幾？

常規法：

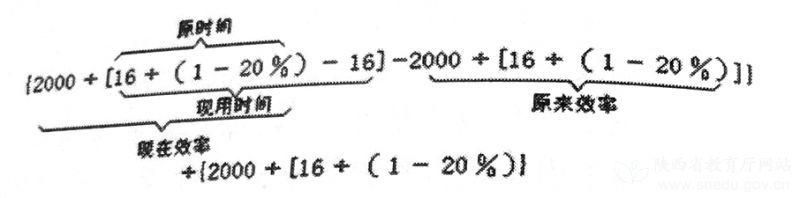
倒數法： 將2000米的工作量看作單位“1”，則工作效率和所需時間互為倒數。當原來所用時間為“1”時，每小時的工作效率也為“1”；第二次修2000米時只用了原時間的20%，這樣每小時的工作效率則為原來的1÷20%倍，所以工作效率比原來增加了：1÷20%-1=4×100%=400%。

評注：乘積為1的兩個數互為倒數，所以將2000米的工作量看作單位“1”，則工作效率和所需時間互為倒數。在此問題中，用常規方法，解題思路復雜，運算繁瑣，易于出錯，而巧用倒數法求解，不僅節省了解題時間，而且大大提高了解題速度和效率。

總之，倒數法是小學數學解題中至關重要的思維方法和解題策略，在小學數學教學中，當采用常規解法過于復雜或存在一定難度時，應善于引導學生打破常規思維束縛，轉換思考角度，另辟蹊徑，求異創新，巧用倒數法妙解數學應用題，從而開拓思路，培養學生思維靈活性和創造性，幫助學生突破解題難關，提高學生數學解題能力。