[摘 要] 目的：為了應(yīng)對(duì)基礎(chǔ)數(shù)學(xué)課程改革的不斷推進(jìn)和教師專業(yè)化水平提升的要求，師范類數(shù)學(xué)教育專業(yè)的教學(xué)需要進(jìn)行著眼于PCK提升的改革。方法：文獻(xiàn)考證與理論分析。結(jié)果：數(shù)學(xué)史指導(dǎo)并豐富教師的課堂教學(xué)，促進(jìn)數(shù)學(xué)師范生對(duì)數(shù)學(xué)的理解和對(duì)數(shù)學(xué)價(jià)值的認(rèn)識(shí)。結(jié)論：數(shù)學(xué)史與高等數(shù)學(xué)教學(xué)的融合，是建構(gòu)師范生PCK知識(shí)的一條有效途徑。

[關(guān)鍵詞] 數(shù)學(xué)師范生 PCK 建構(gòu) 數(shù)學(xué)史 高等數(shù)學(xué)教學(xué) 融合

基金項(xiàng)目：陜西省科學(xué)技術(shù)廳軟科學(xué)項(xiàng)目（2008KR96）；陜西省科學(xué)技術(shù)廳軟科學(xué)項(xiàng)目（2011KMR84）；陜西省教育科學(xué)“十一五”規(guī)劃2010年立項(xiàng)課題（SGH10185）；陜西教育學(xué)院師資培訓(xùn)科研基金項(xiàng)目：（10SX18）。

教師的PCK 是1986年時(shí)任美國(guó)教育研究會(huì)主席的斯坦福大學(xué)教授舒爾曼（Shulman）針對(duì)當(dāng)時(shí)美國(guó)教師資格認(rèn)證制度的缺失而提出來(lái)的一個(gè)重要概念，PCK( Pedagogical Content Knowledge) 即學(xué)科教學(xué)知識(shí)。他認(rèn)為這種知識(shí)是學(xué)科知識(shí)在教學(xué)應(yīng)用中的轉(zhuǎn)換形式, 是特定的內(nèi)容與教學(xué)法的整合或轉(zhuǎn)換, 是教師獨(dú)特的知識(shí)領(lǐng)域,是他們專業(yè)理解的特殊形式。具體來(lái)說(shuō), 就是“對(duì)于一個(gè)人的學(xué)科領(lǐng)域中最一般地要教授的內(nèi)容, 表達(dá)那些概念的最有用的形式, 最有效的比喻、說(shuō)明、例子、解釋以及演示, 一句話, 就是使人易于懂得該學(xué)科內(nèi)容的表達(dá)和闡述方式”,它還包括“知道不同年齡和背景的學(xué)生在學(xué)習(xí)那些最經(jīng)常教授的課題時(shí)己具有的一些日常概念和先入之見(jiàn),這些日常概念和先入之見(jiàn)會(huì)使具體內(nèi)容的學(xué)習(xí)變得容易或困難”[1]。

對(duì)PCK 這種 “能夠幫助教師去建構(gòu)課程內(nèi)容,使教師知道怎樣運(yùn)用有效的類比(analogies) 、舉例(illustrations) 、講解(explanations) 和演示( demonstrations) 的方法來(lái)呈現(xiàn)學(xué)科內(nèi)容,理解和預(yù)想學(xué)生進(jìn)入學(xué)習(xí)過(guò)程時(shí)所擁有的概念和可能存在的困難等的知識(shí)”[2] ，自提出之后, 即成為世界教師教育研究的熱點(diǎn)。 舒爾曼后來(lái)又重新定義了PCK, 認(rèn)為它是教師在面對(duì)特定的學(xué)科課題時(shí), 如何針對(duì)學(xué)生的不同興趣與能力, 將學(xué)科知識(shí)組織、調(diào)整與呈現(xiàn), 以進(jìn)行有效教學(xué)的知識(shí)。這是一種使得教師與學(xué)科專家有所區(qū)別的專門知識(shí)。[3]

我國(guó)學(xué)者也從教學(xué)設(shè)計(jì)(包括目標(biāo)、內(nèi)容、對(duì)象、策略四要素) 和課堂教學(xué)(包括過(guò)程、方法、效果三要素) 等方面比較了小學(xué)數(shù)學(xué)新手和專家教師的PCK,并由此提出: PCK 的實(shí)質(zhì)是一種“轉(zhuǎn)化”的智能,是教師將學(xué)科知識(shí)“轉(zhuǎn)化”成學(xué)生有效獲得的一種學(xué)科教學(xué)智能,即教師根據(jù)課程理念、目標(biāo),進(jìn)行系統(tǒng)思考,把學(xué)科知識(shí)有效地“轉(zhuǎn)化”成教學(xué)任務(wù),又由教學(xué)任務(wù)有效地“轉(zhuǎn)化”為學(xué)生實(shí)際的獲得……相比之下，專家教師能正確把握學(xué)生掌握知識(shí)的情況,并成功地把學(xué)科知識(shí)轉(zhuǎn)化為學(xué)生的實(shí)際所得[4] 。

不難發(fā)現(xiàn)，國(guó)內(nèi)外對(duì)PCK研究的共同點(diǎn)是：它是教師在教學(xué)情境中教師學(xué)科知識(shí)的轉(zhuǎn)化形式。轉(zhuǎn)化的程度是衡量教師專業(yè)化發(fā)展水平的一個(gè)指標(biāo)。特別是在《國(guó)家中長(zhǎng)期教育改革與發(fā)展規(guī)劃綱要》頒布之后，有高素質(zhì)的教師隊(duì)伍，才有高質(zhì)量的教育教學(xué)，已成為社會(huì)公眾的共識(shí)。對(duì)承擔(dān)職前教師培養(yǎng)任務(wù)的師范院校來(lái)說(shuō)，如何提高師范生的職業(yè)能力，使職前培養(yǎng)對(duì)職后專業(yè)化水平提升的效用更大，成了亟待研究的重大課題。本文是從建構(gòu)數(shù)學(xué)師范生PCK的視角，對(duì)數(shù)學(xué)師范生PCK建構(gòu)與數(shù)學(xué)史、高等數(shù)學(xué)教學(xué)融合關(guān)系的思考，以期通過(guò)提高職前數(shù)學(xué)專業(yè)課教學(xué)的有效性，為數(shù)學(xué)師范生奠定職后“轉(zhuǎn)化”的基礎(chǔ)。

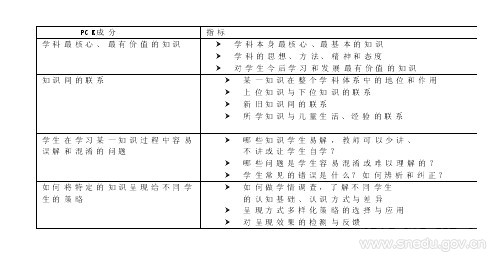
教師PCK的主要成分（出自華東師大數(shù)學(xué)系鮑建生教授的講課稿)

數(shù)學(xué)師范生PCK獲得途徑的分析

學(xué)科最核心、最有價(jià)值的知識(shí)；知識(shí)間的聯(lián)系；這兩部分知識(shí)主要通過(guò)數(shù)學(xué)專業(yè)知識(shí)的學(xué)習(xí)和對(duì)中學(xué)教材研究課程的學(xué)習(xí)獲得。如何將特定的知識(shí)呈現(xiàn)給不同學(xué)生的策略，這部分知識(shí)在校期間可以通過(guò)調(diào)動(dòng)個(gè)人學(xué)習(xí)體驗(yàn)、反思學(xué)習(xí)經(jīng)驗(yàn)和教學(xué)案例，有關(guān)教學(xué)、學(xué)習(xí)、課程理論知識(shí)的學(xué)習(xí)及基本教學(xué)技能的訓(xùn)練，教育見(jiàn)習(xí)等途徑獲得。至于學(xué)生在學(xué)習(xí)某一知識(shí)過(guò)程中容易誤解和混淆的問(wèn)題則在教育實(shí)習(xí)中，通過(guò)搜集學(xué)生對(duì)某一知識(shí)點(diǎn)學(xué)習(xí)的錯(cuò)誤及其成因分析和對(duì)策研究，初步體驗(yàn)獲得這一部分知識(shí)的方式和手段。

再分析學(xué)科最核心、最有價(jià)值的知識(shí)；知識(shí)間的聯(lián)系這兩部分知識(shí)的獲得的方式——聽課和自學(xué)。其中聽課的質(zhì)量是關(guān)乎這兩方面知識(shí)獲得的決定因素。如果一個(gè)師范生在大學(xué)基礎(chǔ)課程學(xué)習(xí)的過(guò)程中，接收的都是經(jīng)過(guò)加工的、完善的、最終的數(shù)學(xué)結(jié)果和形式，而欠缺對(duì)數(shù)學(xué)知識(shí)產(chǎn)生背景的了解、數(shù)學(xué)家進(jìn)行數(shù)學(xué)創(chuàng)造過(guò)程的體悟，這種缺失對(duì)學(xué)生而言，很難對(duì)數(shù)學(xué)形成一個(gè)較為完整的認(rèn)識(shí)，影響學(xué)生形成正確的數(shù)學(xué)觀，和數(shù)學(xué)探究的意識(shí)和興趣。這樣的師范生，日后在教學(xué)實(shí)踐中，怎么可能幫助自己的學(xué)生在自主探究的數(shù)學(xué)學(xué)習(xí)中，體驗(yàn)數(shù)學(xué)學(xué)習(xí)的成功，激發(fā)起繼續(xù)學(xué)習(xí)數(shù)學(xué)的信心和勇氣，建立起較高的數(shù)學(xué)學(xué)習(xí)的自我效能感，從而養(yǎng)成自信、主動(dòng)、質(zhì)疑等良好的個(gè)性品質(zhì)，為學(xué)生未來(lái)幸福的生活奠定一生的基礎(chǔ)。另外，學(xué)生學(xué)習(xí)的不成功，做教師的幸福感從何而來(lái)？一個(gè)沒(méi)有幸福感的人，其生活質(zhì)量從何談起？

再者，教師的一個(gè)重要職責(zé)是為學(xué)生解惑，解惑的前提是要知惑，雖然對(duì)學(xué)生某一知識(shí)過(guò)程中容易誤解和混淆的問(wèn)題這一部分知識(shí)，師范生可以結(jié)合自己的學(xué)習(xí)體驗(yàn)和教育實(shí)習(xí)中的積累加以豐富。但是，在課程學(xué)習(xí)中，教師向師范生展示歷史上數(shù)學(xué)家的一些錯(cuò)誤認(rèn)識(shí)，也可以幫助這些未來(lái)教師把握學(xué)生的疑惑之處。

教育取向的數(shù)學(xué)史研究對(duì)數(shù)學(xué)教育的啟示

文化是一切非自然的、由人類所創(chuàng)造的事物或?qū)ο蟆１娝苤瑪?shù)學(xué)的對(duì)象并不是自然界的客觀實(shí)在物，是數(shù)學(xué)家在長(zhǎng)期實(shí)踐中創(chuàng)造出來(lái)的，因此，數(shù)學(xué)是一種文化。文化的一個(gè)重要特征就是具有歷史性，數(shù)學(xué)也不例外，任何時(shí)期的某一數(shù)學(xué)成果都不是某一時(shí)間的偶然產(chǎn)物，都伴隨著歷史的積淀。“數(shù)學(xué)的過(guò)去被永遠(yuǎn)地同化在它的現(xiàn)在和將來(lái)，這使得數(shù)學(xué)成為一個(gè)逐漸積累的科學(xué)。”[5]如何向?qū)W生展示數(shù)學(xué)的歷史性？

19 世紀(jì),德國(guó)生物學(xué)家海克爾( E. Haeckel ,1843-1919) 提出一個(gè)生物發(fā)生學(xué)定律:“個(gè)體發(fā)育史重蹈種族發(fā)展史。”德國(guó)著名數(shù)學(xué)家F. 克萊因(F. Klein , 1849-1925) 認(rèn)為,數(shù)學(xué)教學(xué)至少在原則上要遵循這項(xiàng)定律,因?yàn)榭茖W(xué)的教學(xué)方法只是誘導(dǎo)人去作科學(xué)的思考,而不是一開頭就教人去碰冷漠的、經(jīng)過(guò)科學(xué)洗練的系統(tǒng)。按照歷史順序教授數(shù)學(xué),能使學(xué)生“看清一切數(shù)學(xué)觀念的產(chǎn)生是如何遲緩;所有觀念最初出現(xiàn)時(shí),幾乎常是草創(chuàng)的形式,只是經(jīng)過(guò)長(zhǎng)期改進(jìn),才結(jié)晶為確定方法,成為大家熟悉的有系統(tǒng)的形式”。

法國(guó)著名數(shù)學(xué)家龐加萊(H. Poincaré,1854-1912) 主張數(shù)學(xué)課程的內(nèi)容應(yīng)完全按照歷史發(fā)展順序展現(xiàn)給讀者,他說(shuō):“動(dòng)物學(xué)家堅(jiān)持認(rèn)為,在一個(gè)短時(shí)期內(nèi),動(dòng)物胚胎的發(fā)育重蹈所有地質(zhì)年代其祖先們的發(fā)展歷史。人的思維發(fā)展似乎也是如此。教育工作者的任務(wù)就是讓孩子的思維經(jīng)歷其祖先之所經(jīng)歷,迅速通過(guò)某些階段而不跳過(guò)任何階段。鑒于此,科學(xué)史應(yīng)該是我們的指南。”[6]

就像美國(guó)數(shù)學(xué)家和數(shù)學(xué)史家克萊因認(rèn)為的：“每一位中學(xué)和大學(xué)數(shù)學(xué)教師都應(yīng)當(dāng)知道數(shù)學(xué)史，有許多理由，但最重要用的一條理由或許是：數(shù)學(xué)史是教學(xué)的指南。”[7]

另外，西方學(xué)者對(duì)數(shù)學(xué)史數(shù)學(xué)功能的觀點(diǎn)，汪曉勤教授在《古為今用：美國(guó)學(xué)者眼中數(shù)學(xué)史的教育價(jià)值》一文中總結(jié)為：1.數(shù)學(xué)史激發(fā)學(xué)生的興趣，改變學(xué)生的數(shù)學(xué)觀；2.數(shù)學(xué)原始文獻(xiàn)的價(jià)值；3.數(shù)學(xué)史使數(shù)學(xué)人性化；4.數(shù)學(xué)家遇到的困難和挫折，同樣也會(huì)為課堂上的學(xué)生所經(jīng)歷；5.學(xué)生學(xué)習(xí)數(shù)學(xué)的認(rèn)知過(guò)程與數(shù)學(xué)史的發(fā)展過(guò)程相似；6.數(shù)學(xué)史幫助學(xué)生理解和欣賞數(shù)學(xué)；7.歷史上的數(shù)學(xué)問(wèn)題提供了豐富的社會(huì)文化信息。[8]等等，這些研究成果都啟示我們，數(shù)學(xué)教學(xué)不能就數(shù)學(xué)講數(shù)學(xué)，應(yīng)該向?qū)W生展現(xiàn)歷史上數(shù)學(xué)的知識(shí)、思想、方法產(chǎn)生過(guò)程中數(shù)學(xué)家的艱辛付出和火熱的思考，告別只留下干巴巴框架的數(shù)學(xué)教學(xué)。通過(guò)對(duì)數(shù)學(xué)的演進(jìn)與變革的了解，幫助未來(lái)的教師更好地理解數(shù)學(xué)，使他們這些未來(lái)教數(shù)學(xué)的人先感受到數(shù)學(xué)的親切，才可能談及傳播親切的數(shù)學(xué)。

數(shù)學(xué)史與高等數(shù)學(xué)專業(yè)課教學(xué)融合

愛(ài)好數(shù)學(xué)是教好數(shù)學(xué)的一個(gè)重要前提。高等數(shù)學(xué)學(xué)習(xí)的內(nèi)容、方法、困難的程度與基礎(chǔ)教育學(xué)段的數(shù)學(xué)有很大不同。如何幫助師范生保持對(duì)數(shù)學(xué)的喜愛(ài)、對(duì)數(shù)學(xué)問(wèn)題探究的熱情？如何加快適應(yīng)高等數(shù)學(xué)的學(xué)習(xí)？首先，要針對(duì)高等數(shù)學(xué)的抽象性，克服知識(shí)的“天外之物性”，在教學(xué)中要對(duì)知識(shí)產(chǎn)生的合理性進(jìn)行設(shè)計(jì)。為此，在數(shù)學(xué)師范生基礎(chǔ)專業(yè)課的學(xué)習(xí)過(guò)程中，可恰當(dāng)?shù)亟柚恍?shù)學(xué)史的知識(shí)，如微積分中導(dǎo)數(shù)概念的引入，介紹一下為什么人們當(dāng)時(shí)要研究切線？讓師范生認(rèn)識(shí)到所引入的新主題乃是解決問(wèn)題之需要,讓他們產(chǎn)生足夠的動(dòng)機(jī)，從而獲得良好的學(xué)習(xí)效果。講洛比達(dá)法則時(shí)，介紹一下當(dāng)年發(fā)生在法則背后的故事，一來(lái)讓師范生感受數(shù)學(xué)家也是凡人，二來(lái)加深了對(duì)定理的印象。學(xué)習(xí)泰勒展開式時(shí)講點(diǎn)數(shù)學(xué)史上張冠李戴的故事，學(xué)習(xí)隱函數(shù)求導(dǎo)時(shí)講點(diǎn)“業(yè)余數(shù)學(xué)家戰(zhàn)勝了專業(yè)數(shù)學(xué)家”的引子等等，幫助師范生樹立學(xué)習(xí)數(shù)學(xué)的良好情感，認(rèn)識(shí)到“數(shù)學(xué)不過(guò)是人類的一種文化活動(dòng),人人可學(xué),人人可做,盡管并非人人都有數(shù)學(xué)家的才能;而從事這種文化活動(dòng)的數(shù)學(xué)家也是平凡的人,同樣會(huì)遇到困難、挫折、失敗。了解這一點(diǎn),師范生就不會(huì)為自己在學(xué)習(xí)過(guò)程中所遇困難、挫折和失敗而灰心喪氣,甚至錯(cuò)誤地認(rèn)為自己沒(méi)有數(shù)學(xué)頭腦了”。[9]同時(shí)，經(jīng)歷了體現(xiàn)數(shù)學(xué)歷史性的教學(xué)，師范生才能樹立真正關(guān)注學(xué)生數(shù)學(xué)情感的意識(shí)，寬容、平靜地對(duì)待學(xué)生的錯(cuò)誤，并給學(xué)生予以修正錯(cuò)誤的時(shí)間。與此同時(shí)，增強(qiáng)了自己有關(guān)對(duì)學(xué)生學(xué)習(xí)某一知識(shí)過(guò)程中容易誤解和混淆的問(wèn)題的把握能力，豐富了自己如何辨析與糾正學(xué)生存在問(wèn)題的策略。在某種程度上是對(duì)未來(lái)從教所需PCK的一種積累。

另外，有了數(shù)學(xué)史與高等數(shù)學(xué)的融合，數(shù)學(xué)師范生在學(xué)好基礎(chǔ)課程的同時(shí)，還會(huì)習(xí)得一種到數(shù)學(xué)史的寶藏中尋寶的習(xí)慣，不僅豐富了自己的數(shù)學(xué)文化素養(yǎng)，也無(wú)形中獲得了一種教學(xué)的策略，同時(shí)，從歷史上數(shù)學(xué)家對(duì)數(shù)學(xué)知識(shí)理解的偏差，獲得自己教學(xué)設(shè)計(jì)中對(duì)學(xué)生認(rèn)知難度的理解，會(huì)更多地思考學(xué)生可能的困難和疑惑，從而提高教學(xué)的有效性。

綜上，數(shù)學(xué)史更多地融合于師范生基礎(chǔ)專業(yè)課的學(xué)習(xí)，有利于形成師范生良好的數(shù)學(xué)學(xué)習(xí)情感和動(dòng)態(tài)可謬的數(shù)學(xué)觀；形成追問(wèn)知識(shí)發(fā)生、發(fā)展過(guò)程的習(xí)慣；能從歷史相似性和歷史發(fā)生教學(xué)法的角度來(lái)設(shè)計(jì)高速重演數(shù)學(xué)知識(shí)發(fā)生發(fā)展過(guò)程的教學(xué)；因?yàn)榘盐諏W(xué)生學(xué)習(xí)產(chǎn)生困難和犯錯(cuò)誤的困惑，而給學(xué)生更多理解，為學(xué)生預(yù)留了更大的生成空間，同時(shí)，對(duì)學(xué)生更多的理解，還有助于形成良好的師生關(guān)系，讓學(xué)生因親其師而信其道，使這些未來(lái)教師可以盡早地獲得教學(xué)的成功。然而，正確的數(shù)學(xué)觀、對(duì)知識(shí)來(lái)龍去脈的追問(wèn)習(xí)慣、對(duì)學(xué)生易出錯(cuò)和困惑的把握、主動(dòng)思考學(xué)情去尋找學(xué)生最易接受的比喻、說(shuō)明、例子、解釋以及演示等素養(yǎng)，恰恰都是支撐師范生將來(lái)向成功教師邁進(jìn)的PCK。所以，數(shù)學(xué)史與高等數(shù)學(xué)教學(xué)的融合是師范生建構(gòu)PCK的有效途徑。

參考文獻(xiàn)：

[1]Shulman.L.(1986).Those Who Understand Knowledge in teaching .Education Reseacher.15(2).PP.9.

[2]袁維新.學(xué)科教學(xué)知識(shí):一個(gè)教師專業(yè)發(fā)展的新視角[J].外國(guó)教育研究,2005,3:10-14.

[3]楊彩霞. 教師學(xué)科教學(xué)知識(shí):本質(zhì)、特征與結(jié)構(gòu)[J].教育科學(xué),2006,22(1)：60-63.

[4]上海市青浦實(shí)驗(yàn)研究所(2007).小學(xué)數(shù)學(xué)新手和專家教師PCK 比較的個(gè)案研究[J].上海教育科研,2007(10):55-58.

[5]馮振舉，戴麗麗.國(guó)際HPM的發(fā)展歷程及啟示[J].西北大學(xué)學(xué)報(bào)(自然科學(xué)版)，2005，35（5）：654-656.

[6]Kline M. Logic Versus Pedagogy[J]. American Mathematical Monthly ,1970 ,77(3):264-282.

[7]克萊因M.古今數(shù)學(xué)思想(第1冊(cè))[M].張里京，譯.上海：上海科學(xué)技術(shù)出版社，1979：2-3.

[8][9]汪曉勤,林永偉.古為今用：美國(guó)學(xué)者眼中數(shù)學(xué)史的教育價(jià)值[J].自然辯證法研究，2004（6）：73-76.