推理是數(shù)學(xué)的重要組成部分，在小學(xué)數(shù)學(xué)教學(xué)中學(xué)生推理能力的培養(yǎng)很有必要，下文就如何在小學(xué)教學(xué)中培養(yǎng)學(xué)生的推理能力進(jìn)行了簡要的分析。

一、推理的概述

推理是由已知推斷出未知結(jié)論的過程，它是一種形式邏輯，通過推理，我們可以從已知的知識(shí)中獲得未知的知識(shí)，特別是那些通過感覺和經(jīng)驗(yàn)得不到的未知知識(shí)。推理分為演繹推理和歸納推理。演繹推理是從一般到特殊的過程，從一般規(guī)律出發(fā)，運(yùn)用邏輯證明和數(shù)學(xué)運(yùn)算得出特殊事項(xiàng)的規(guī)律；歸納推理是從特殊到一般的過程，從許多個(gè)別事件中總結(jié)歸納出一般性的規(guī)律。

推理是一個(gè)科學(xué)的思維過程，人們在探索新知識(shí)的時(shí)候離不開推理這種思維方式。在學(xué)習(xí)中，需要通過邏輯推理的思維活動(dòng)把已知和未知的知識(shí)聯(lián)系起來，從而構(gòu)建起溝通已知知識(shí)和未知知識(shí)之間的橋梁。已知知識(shí)是推理的前提，人們通過邏輯推理得出未知的結(jié)論。經(jīng)常開展邏輯推理的思維活動(dòng)有利于人們科學(xué)系統(tǒng)的理解知識(shí)和開發(fā)智力。

二、推理能力在小學(xué)數(shù)學(xué)教學(xué)中的重要性

推理過程其實(shí)是分析矛盾的過程，這個(gè)過程對(duì)學(xué)生理解知識(shí)和開發(fā)智力有著積極的作用。推理能力的作用還表現(xiàn)在日常生活中解決問題的能力上，生活中遇到任何問題都應(yīng)該進(jìn)行冷靜的思考，對(duì)其進(jìn)行分析判斷，從而得出解決問題的辦法。而小學(xué)教學(xué)中可以發(fā)現(xiàn)，學(xué)生成績是由解決問題的能力所決定，解決問題能力高的學(xué)生成績通常都不會(huì)很差，而解決問題能力差的學(xué)生成績通常都很差。所謂解決問題能力差是指學(xué)生無法運(yùn)用自己所學(xué)的知識(shí)，他們只會(huì)學(xué)習(xí)，卻不會(huì)實(shí)際運(yùn)用，這種情形下，學(xué)習(xí)對(duì)他們而言則毫無意義。

數(shù)學(xué)是一門演繹的科學(xué)，推理是數(shù)學(xué)的基本要素之一。在小學(xué)數(shù)學(xué)教學(xué)中，教師應(yīng)注重培養(yǎng)學(xué)生的推理能力，引導(dǎo)學(xué)生在數(shù)學(xué)學(xué)習(xí)過程中從觀察到實(shí)驗(yàn)再到猜想最后得出結(jié)論。必須讓學(xué)生學(xué)會(huì)合情推理并初步養(yǎng)成演繹推理的習(xí)慣，在實(shí)際生活中，當(dāng)他們遇到各種實(shí)例，便會(huì)自己去嘗試思考分析、主動(dòng)去尋求答案，他們在探索答案的過程中，會(huì)享受到思維的樂趣，獲得成就感，這樣便會(huì)逐步養(yǎng)成良好的學(xué)習(xí)習(xí)慣并同時(shí)提高他們的學(xué)習(xí)能力。所以，培養(yǎng)學(xué)生的推理能力在小學(xué)數(shù)學(xué)教學(xué)顯得格外重要。

三、如何在小學(xué)數(shù)學(xué)教學(xué)中培養(yǎng)學(xué)生推理能力

1.首先應(yīng)培養(yǎng)學(xué)生對(duì)推理的興趣，給學(xué)生提供推理的空間

在教學(xué)中，首先應(yīng)做的是培養(yǎng)學(xué)生對(duì)學(xué)習(xí)的興趣，學(xué)生對(duì)所學(xué)的知識(shí)感興趣之后才能夠激發(fā)他們學(xué)習(xí)的熱情，進(jìn)而樂于 去學(xué)習(xí)探索，從而達(dá)到事半功倍的效果。

數(shù)學(xué)推理能力源于數(shù)學(xué)猜想，大膽地去猜想，然后去探究猜想的正確性，不斷修正，最后得出證明。作為數(shù)學(xué)老師，在日常數(shù)學(xué)教學(xué)中應(yīng)該試著將碰到的各種問題交由學(xué)生自己來解決，給他們提供寬松的學(xué)習(xí)環(huán)境，讓他們有足夠的時(shí)間和空間去自由地思考問題，以此鼓勵(lì)學(xué)生們進(jìn)行猜想，激發(fā)他們探索發(fā)現(xiàn)的興趣，讓他們學(xué)會(huì)思考并樂于思考，通過實(shí)驗(yàn)、歸納、同類比較等方法去驗(yàn)證他們的各種猜想，從而得出解決問題的方法。在這個(gè)過程之中，學(xué)生們不斷地探索發(fā)現(xiàn)，新的方法、新的思路不斷涌現(xiàn)，邏輯思維能力不斷得到提高，這些都給學(xué)生們推理能力的提高打下堅(jiān)實(shí)的基礎(chǔ)。

2.將教學(xué)融入生活，寓教于樂，結(jié)合實(shí)際引導(dǎo)學(xué)生進(jìn)行推理

數(shù)學(xué)不僅僅只是由枯燥無味的數(shù)學(xué)法則、性質(zhì)、公式等組成，它也可以具有趣味性和多樣性。小學(xué)數(shù)學(xué)其實(shí)是跟生活密不可分的，日常生活中的一切都要用到數(shù)學(xué)，數(shù)學(xué)來源于生活，作為教師，應(yīng)該善于利用這一點(diǎn)，從而讓數(shù)學(xué)教學(xué)不再枯燥無味。下面結(jié)合幾個(gè)實(shí)例簡要敘述一下如何在實(shí)際教學(xué)中培養(yǎng)學(xué)生的推理能力。

譬如，圓錐體的體積=底面積×高×1/3，圓柱體的體積=底面積×高，由此可以看出相同底面積和高度的圓錐體的體積是圓柱體的1/3，但為什么是1/3呢？為什么不是1/2或者1/4呢？老師可以向?qū)W生提出這樣的疑問，既然有了疑問，那么便可以用事實(shí)來驗(yàn)證這個(gè)結(jié)論是否正確。老師可以讓學(xué)生們自己動(dòng)手做出相同底面積相同高度的圓柱體和圓錐體容器，接下來就很簡單了，將圓錐體容器裝滿沙子倒進(jìn)圓柱體容器中，3次恰好裝滿圓柱體容器便證明了這個(gè)結(jié)論是正確的。

通過這個(gè)小小的實(shí)驗(yàn)，學(xué)生們首先加強(qiáng)了對(duì)圓柱體和圓錐體的認(rèn)知，對(duì)于他們來說這兩個(gè)名詞不再僅是空洞的概念，而是具有直觀的形象；其次，他們明白了圓錐體和圓柱體之間的聯(lián)系，通過自己懷疑——驗(yàn)證這個(gè)推理過程得出的結(jié)論讓他們印象深刻。由抽象的公式到具體的實(shí)驗(yàn)驗(yàn)證，思維由淺入深，有利于他們推理能力的提高；最后，直觀的實(shí)驗(yàn)過程提高了他們學(xué)習(xí)的興趣，以后再碰到類似的問題，他們便會(huì)樂于自己去解決該類問題，在發(fā)現(xiàn)問題解決問題的過程中，他們的各項(xiàng)能力都得到鍛煉。

再例如，現(xiàn)在有7個(gè)硬幣，將其進(jìn)行排列，請問如何排才能使在同一條直線上有三枚硬幣的直線數(shù)最多？這是一道趣味性比較強(qiáng)的題目，可以讓學(xué)生們自己動(dòng)手嘗試，用7個(gè)硬幣擺出答案。題目的要求是一條直線上有3個(gè)硬幣，所以學(xué)生們肯定不會(huì)像下面這樣排成一條直線，這種排列方法，有3個(gè)硬幣的直線數(shù)為零。

既然是3個(gè)一排，那么最簡單的想法是先拿出6個(gè)硬幣，3個(gè)一排，排成并列的兩排，剩下一個(gè)再搭配下便又形成了一條直線，如下圖所示：

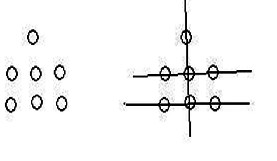
但是，這樣的排列方法下，兩邊的硬幣沒有得到充分的利用，稍微將最下面一排左右兩枚硬幣往外移一點(diǎn)便是另外一種結(jié)果，如下圖：

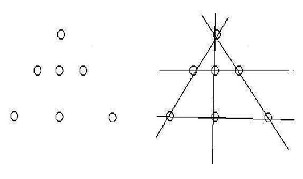
這種結(jié)果得到5條直線，那么5條直線是否就是最多的結(jié)果呢，還可以讓學(xué)生們再嘗試移動(dòng)硬幣，看是否可以得到更多的直線，經(jīng)過試驗(yàn)之后，我們可以發(fā)現(xiàn)，將最中間的那枚硬幣稍微往下移一點(diǎn)之后，我們便可以獲得6條直線，見下圖：

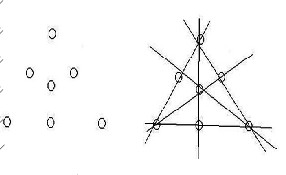
通過這個(gè)過程，學(xué)生們可以從中獲得不斷探索發(fā)現(xiàn)的樂趣，在探索中逐步靠近正確的答案。

最后一個(gè)例子，甲乙兩人在一張桌子上玩擺棋子游戲，每次擺一顆，兩人輪流擺下去，棋子不能重疊，不能移動(dòng)，也不能超出桌子范圍，最后誰擺不下棋子誰就輸。問先擺的那個(gè)人放在哪個(gè)位置一定會(huì)贏？這道題目的答案是事先擺在正中心，然后對(duì)方在哪擺你就在其對(duì)稱位置擺放。這個(gè)答案看上去很正確，且不說實(shí)際操作如何，單從理論上看還是行得通的。可是這個(gè)論題本身卻是一個(gè)偽命題，我們假設(shè)這張桌子不斷縮小，直至縮到只有一個(gè)棋子那么大，那么先放的那個(gè)人放上去就直接贏了，后放的那個(gè)人根本就是沒有參與就直接宣告出局，所以說這個(gè)題目本身就沒有意義，單純只為出題而出題，實(shí)屬偽推理，像這種題目對(duì)于學(xué)生來說，并不能培養(yǎng)他們的推理能力。

所以在小學(xué)數(shù)學(xué)教學(xué)中培養(yǎng)學(xué)生推理能力的同時(shí)，還應(yīng)注意一點(diǎn)，那就是避免為了推理而推理。學(xué)生推理能力的培養(yǎng)重在過程而并非片面追求結(jié)果， 凡事皆有度，過猶不及，能力的養(yǎng)成不在一朝一夕。對(duì)于老師來說，切忌用大量的具有推理性的題目來訓(xùn)練學(xué)生的推理能力。這些題目做得多了，學(xué)生自會(huì)形成條件反射，可以很輕松地解答類似的題目，可同時(shí)卻也存在著隱患，那就是在做普通數(shù)學(xué)題時(shí)不免會(huì)將簡單問題復(fù)雜化，審題的時(shí)候思路總是要繞幾個(gè)圈子，有時(shí)繞著繞著便把自己繞進(jìn)去了。因此，用大量數(shù)學(xué)題來提高學(xué)生的推理能力這種方法并不可取。老師應(yīng)教給學(xué)生思考的方法，讓他們自己去思考判斷，而非教給他們解題的思路模板，這樣容易形成定向思維，極不利于學(xué)生推理能力的發(fā)展。

四、總結(jié)

小學(xué)生推理能力的培養(yǎng)是一個(gè)逐步推進(jìn)的過程，在這個(gè)過程中，教師首先要激發(fā)學(xué)生去大膽猜想，在學(xué)生驗(yàn)證猜想的過程中進(jìn)行適當(dāng)指引，鼓勵(lì)支持他們的奇思妙想但同時(shí)也要及時(shí)糾正他們不切實(shí)際的猜測。學(xué)生和老師的緊密配合，不斷提出猜想、驗(yàn)證猜想、修正猜想、得出結(jié)論，良性循環(huán)，學(xué)生們在探索的過程中進(jìn)行創(chuàng)造，親身感受了驗(yàn)證和證明的重要性。在這個(gè)過程中，學(xué)生們接觸到很多的學(xué)習(xí)材料，并養(yǎng)成良好的思維習(xí)慣，樂于去發(fā)現(xiàn)問題并解決問題，逐漸領(lǐng)悟到各種知識(shí)，提升自己各項(xiàng)學(xué)習(xí)能力。

推理能力的培養(yǎng)不僅僅是提高了學(xué)生的學(xué)習(xí)成績，更重要的是可以提升學(xué)生解決問題的能力，使他們在學(xué)習(xí)以及生活中可以從容面對(duì)各種困難，通過邏輯分析準(zhǔn)確判斷從而解決這些難題。作為老師來說，教給學(xué)生學(xué)會(huì)推理遠(yuǎn)比教給學(xué)生知識(shí)更為重要，正所謂授人以魚不如授人以漁，同時(shí)學(xué)生學(xué)會(huì)解決問題的思路和方法之后老師的教學(xué)任務(wù)也將減輕。