在小學數學里，經常將某一問題轉化為另一問題，將某些已知條件或數量關系轉化為另外的條件或關系，化生為熟、化難為易、化繁為簡、化高為低、化曲為直，這就是轉化的思想方法。

在小學數學里處處充滿了轉化。例如，平行四邊形的面積公式是轉化為長方形求得的；三角形的面積公式就是轉化為平行四邊形求得的;圓的面積是轉化為長方形的面積求得的；小數乘法、小數除法轉化為整數乘法、整數除法；分數除法是轉化為分數乘法來計算的；異分母分數加減法轉化為同分母分數加減法……轉化思想方法的實質就是在已有的、簡單的、具體的、基本的知識的基礎上，把未知化為已知、把復雜化為簡單、把一般化為特殊、把抽象化為具體、把非常規化為常規，從而解決各種問題。轉化的方法就是等價變形、數形結合、正難則反等。

這是人教版課改新教材小學數學三年級上冊第14頁的圖，是曹沖稱象的故事。

當時為什么大臣們稱不出大象的體重，而曹沖能稱出大象的體重呢？這是因為曹沖成功地運用了“轉化的思想方法”。

使船吃水同樣深淺

稱大象體重———————————稱石頭重量

找出與大象

重量相同的一堆石頭

曹沖把稱大象的體重轉化為稱石頭的重量。“轉化的思想方法”使曹沖創造性地解決了當時條件下難以解決的問題，受到了人們的稱贊。

例1 三階幻方問題。

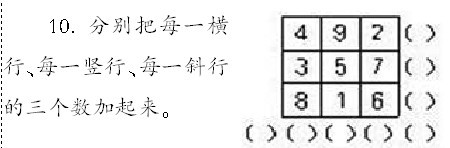
這是人教版小學數學一年級上冊120頁第10題。

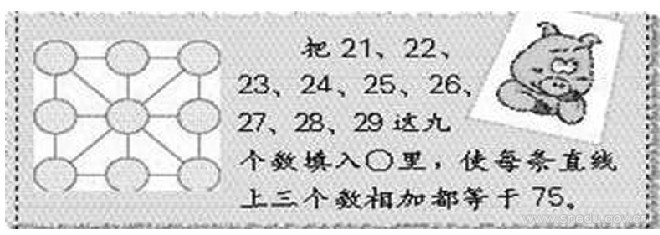
這是人教版小學數學一年級下冊第77頁思考題。

如何填一年級下冊第77頁這一思考題呢？轉化！利用一年級上冊120頁第10題轉化：給1、2、3、…、9每個數加上20，就成為21、22、23、…29。

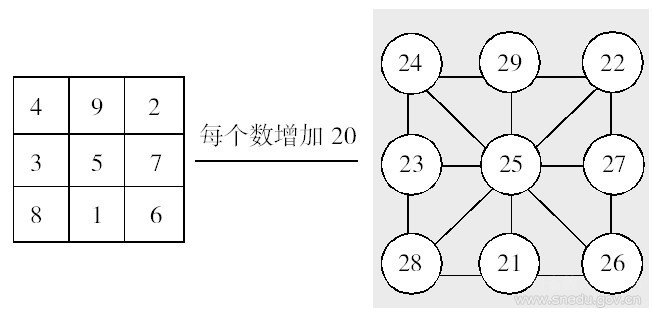
利用轉化，解決了一年級下冊第77頁的思考題。

例2 人教版課標新教材五年級下冊第116頁的13*題。

分母是20，先乘以20轉化為整數填，使每個正方形四個角上的數加起來等于20，最后再把每個數除以20。

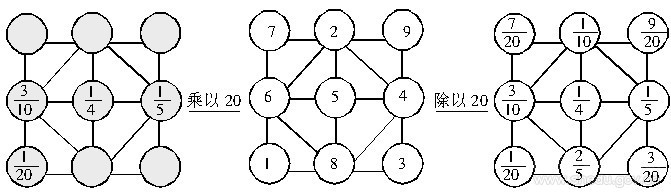
例3 一個鐘每小時慢3分, 照這樣計算, 早上5時對準標準時間后, 當晚上這個鐘指著12時的時候, 標準時間是幾時幾分?

這是人教版小學數學課標教材六年級下冊第87頁的思考題。

解：“一個鐘每小時慢3分”, 就是說當標準鐘表走60分鐘時,慢鐘表才走了自己鐘表的60-3=57分鐘。所以，在相同的時間內，標準鐘表顯示的時間是慢鐘表顯示時間的60/57。

從“早上5時對準標準時間后”，到“當晚上這個鐘指著12時的時候”，慢鐘表走了自己鐘表的24-5=19小時。所以，從“早上5時對準標準時間后”，到“當晚上這個鐘指著12時的時候”，標準鐘表走了60/57×19=20小時，標準時間恰好是凌晨1時。

如下圖所示。

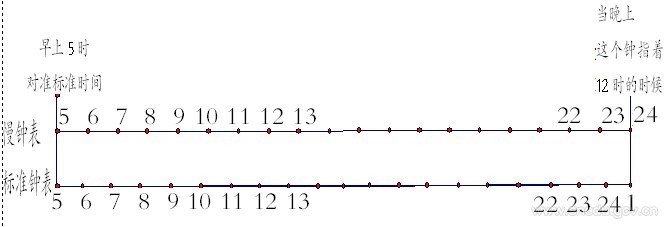
答：標準時間是凌晨1時整。

這里把“一個鐘每小時慢3分”轉化為“在相同的時間內，標準鐘表顯示的時間是慢鐘表顯示時間的60/57”,使原問題得到順利解決。

例4 人教版課標教材五年級下冊第32頁的9*題。

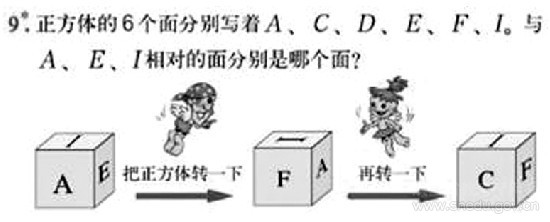
解: 首先考慮與I相對的面是哪一面?

正難則反, 我們從“與I相對的面不是哪一面”入手。從圖可知：與I相對的面不是A、E、F、C，只剩下D面，所以與I相對的面是D。

與A相對的面不是I、D、E、F，只剩下C面，所以與A相對的面是C。

與E相對的面是F。

正難則反也是轉化的有效方法之一。

例5 人民教育出版社新課標教材四年級上冊第48頁的思考題。

解：由于要使三角形每條邊上3個數的積都相等，給10、15、20、30、40、60這六個數每個數都除以10，只需要考慮1、1.5、2、3、4、6這六個數。問題轉化為：

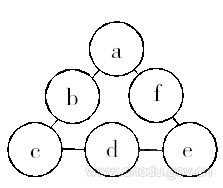
將1、1.5、2、3、4、6填入上圖圓圈內，使三角形每條邊上3個數的積都相等。

假設如圖是滿足題設條件的填法。a、b、c、d、e、f是1、1.5、2、3、4、6中的數。由于a×b×c = c×d×e = e×f×a = A,所以a×b×c×c×d×e×e×f×a =A3 ，即有：

（a×b×c×d×e×f）×（a×c×e）= A3，但是a×b×c×d×e×f = 1×1.5×2×3×4×6=63, 所以a×c×e =(A/6)3。

由a×c×e =(A/6)3知a×c×e 是一個完全立方數，而在1、1.5、2、3、4、6中只有1×2×4=23，1.5×3×6 =33。所以a、c、e為1、2、4或1.5、3、6。

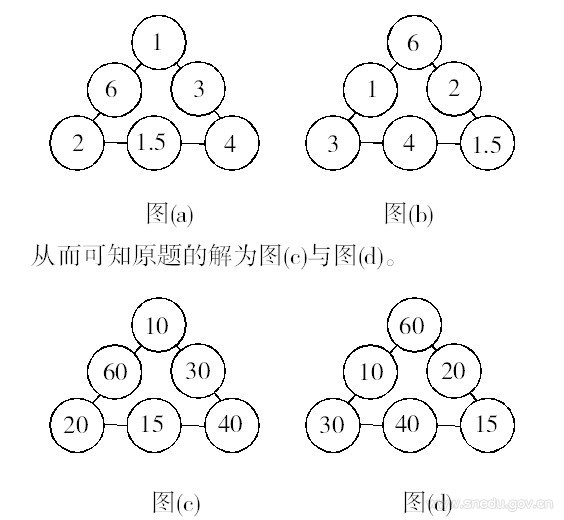
當a、c、e為1、2、4時，由(A/6)3=23知，幻積A=12，可以得到如圖（a）的填法。

當a、c、e為1.5、3、6時，由(A/6)3=33知，幻積A=18，可以得到如圖（b）的填法。

著名數學教育家張奠宙教授指出：“只有把數學思想方法嵌入日常的教學之中，成為教師備課的有機組成部分，四基數學教學才能真正落到實處。”（見《數學教育學報》2011年第5期，張奠宙、鄭振初，“四基”數學模塊教學的構建——兼談數學思想方法的教學）由此可見，深入挖掘數學教材中的數學思想方法是落實“四基”的基礎，每一個數學教師都應該做出自己的努力。