[摘 要] 初學復調容易混淆的幾個概念；復調音樂與主調音樂、支聲音樂的區別；復調旋律在寫作中應注意的幾個問題。

[關鍵詞] 多聲部音樂 主調音樂 復調音樂 支聲音樂 對比式復調 模仿復調 主調音樂的展開部 賦格的展開部

復調音樂屬于多聲部音樂的一種，是音樂院校為作曲與作曲技術理論專業開設的“四大件”中必不可少的一門課程，同時它也是構建音樂大廈的重要材料之一。復調音樂以藤蔓式的橫向線條與基石般的縱向和聲緊密配合，共同營造著音樂作品的立體化音響效果，它與和聲就像人的手背手心，互為表里，誰也離不開誰。在復調的學習中學生很容易混淆一些基本的概念，下面來簡單地談一談：

多聲部音樂、復調音樂和主調音樂

有些初學者以為多聲部音樂就是指復調音樂，這個概念是不正確的。

多聲部音樂泛指包含兩個或兩個以上聲部呈現的音樂形態，它是與單聲部音樂相對應的一個音樂名詞。按已形成的傳統音樂學科分類，研究多聲部音樂的相關學科應包含：和聲學、復調音樂、曲式學、管弦樂配器法、和作曲等。多聲部音樂以縱向上聲部安排的不同方式可分為：復調音樂和主調音樂。因此絕不能錯誤地認為多聲部音樂就是指復調音樂。

復調音樂的概念是兩個或兩個以上具有相對獨立意義和鮮明性格特征的旋律，按照對位法則有機結合而成的多聲部音樂形式。

主調音樂是由若干個附屬聲部運用和弦序進和各種音型化織體的方式（和聲織體），來陪襯、烘托著一個具有獨立性旋律的多聲部音樂形式。例如：各種獨唱歌曲，既有人通過歌詞來演唱旋律，又有鋼琴或樂隊用和聲織體來伴奏，這就是典型的主調音樂。

主調音樂與復調音樂二者在創作中往往是密不可分的，除了完全是以復調手法寫作的作品以外，我們常看到許多典型的主調音樂寫作中結合了一些復調的寫作手法來與主題作對位與呼應，以此來豐富音樂的表現能力。就像阿薩菲耶夫曾經說過的：“和聲在復調音樂中就像被凝結后的熔巖。”塔涅耶夫也曾說：“在優秀的作品中，往往主調音樂結合了復調音樂，因此可以說在任何的音樂中都可以用復調手法來豐富它。”反之，復調的多聲部結合也時刻體現了和聲的基礎，因此研究復調音樂必須很好的學習和聲。無論是主調音樂還是復調音樂它們都屬于多聲部音樂，是創作音樂的不同手法，二者在音樂作品中分別占有不可或缺的重要地位。

復調和對位在概念的不同

在復調音樂寫作中會涉及到一個非常專業的術語“對位”（Counterpoint）。這個詞源于拉丁語（Punctus contra punctus）,直譯就是“點對點”。它是中古時代歐洲宗教音樂家們創用的名詞，在音樂理論里是研究二聲部或更多聲部，在節奏、旋律、和聲等因素結合時的關系問題。也就是具有獨立意義而又彼此和諧的不同旋律的結合。而“對位法”就是寫作對位的技術 。“對位”與“復調”是密切相關的兩個概念，對位法更為具體，更具有技術的內涵。而復調可以作為表現手法，廣泛地運用于各類音樂作品中；也可以作為一種音樂體裁而獨立的構成樂曲，如“卡農曲”、“賦格曲”、“帕薩卡里亞”等都是復調音樂具有代表性的體裁形式。

復調和對位的關系，就如同主調與和聲之間的關系。復調音樂是和主調音樂相對應的兩種不同的音樂表現形式。因此，應該正確地理解和認識較為廣義的“復調”以及較為技術化的“對位”兩個詞的正確含義，而不應把兩者混為一談。

支聲音樂和復調音樂

1）支聲音樂

是指所有的聲部奏同一旋律，而各個聲部會用旋律的不同變形來表現。其中這些變形有多種形態：（①旋律的加花變奏但節奏可能相互對比；②兩個或兩個以上旋律時合時分地同步進行；③旋律用平行手法來寫作，節奏沒有對比）簡單地說，支聲結構是單聲部音樂的一種發展形式，分支音調從主旋律線的總的音調結構中派生出來，是在基本旋律主軸上分化出來的一個支脈。分支聲部與主要旋律的關系屬于同質異體的性質。

正確地認識支聲音樂對于我們學習和寫作復調音樂有著十分重要的幫助。支聲音樂多運用于民族民間音樂中，它也屬于多聲部音樂的一種類型，可以說是多聲部寫作手法的一個較為廣泛而變化多端的范疇。在很多專業的多聲部音樂創作中，也常常會用支聲的手法來展開樂思，并將這一寫作原則不斷地加以擴大、發展，從而更進一步地豐富了支聲音樂這一形式。有時因為支聲復音樂的各個聲部在節奏上有不同甚至對比，很多初學者往往會把它們與對比復調相混淆。換句話說，如果各個聲部間的獨立性增強到能以相互對比或各自獨立為主要特征時，支聲復調也就成為對比復調了。因此，也有些人認為支聲音樂從嚴格意義上來講不屬于復調音樂，有時也會把它們看作是單音音樂向復調音樂的一個過渡。

2）復調音樂包括兩種類型：a.非模仿的復調即對比復調；b.模仿的復調。

a.非模仿的復調——對比復調

對比式復調：是指兩個或兩個以上不同旋律（主要指節奏和旋律特點上）有機結合而成的復調音樂。前面指出初學者有時會把它與支聲復調從形態上弄不清楚，主要原因是它們在節奏上都有所對比，但對比復調除了節奏對比以外，還同時強調不同旋律的對比與有機結合，并且它在節奏上也更加注意幾個聲部之間的動靜結合關系。總之，無論是節奏還是旋律，對比復調在強調對比的同時也仍然遵循相互補充、相互呼應的原則。但是在一些具有特殊情景的音樂中，所運用對比復調手法寫作的主題旋律可能會具有十分鮮明的對抗性，例如：穆索爾斯基創作的鋼琴套曲《圖畫展覽會》中的第六首“兩個猶太人，一個窮一個富”就是運用了兩個截然不同的主題旋律先是分別陳述再進行疊加，來進行形象對比的。這種對比的手法在西方的音樂創作中相對使用較多，然而在具有中國風格的復調音樂的創作中大多數對比復調的音樂整體形象是統一的，聲部之間常常是具有互補性的，它們往往描繪的是人或事物的不同側面。例如：陳剛、何占豪創作的小提琴協奏曲《梁山伯與祝英臺》中的對比旋律，雖然無論從節奏還是旋律上與主題都有對比，但二者并不具有對抗性，它們是在對比的同時又相輔相承、密不可分，這和我們中國人的審美也有著非常緊密的關系。

b.模仿的復調

模仿復調：就是同一旋律或者主題在不同聲部以依次出現的方式有機結合起來的復調音樂。例如：冼星海創作的《黃河大合唱》中的“保衛黃河”。它是一首用模仿復調的手法寫作的三聲部輪唱，后面聲部依次比前面的聲部晚一小節進入，各個聲部的旋律與歌詞都是相同的。模仿式復調包括有：嚴格模仿、變化模仿以及節奏模仿和自由模仿等。而嚴格模仿又包括：局部模仿（簡單模仿）和卡農是模仿。如果模仿聲部對開始聲部陳述的音樂材料不進行連續模仿，就被稱為“局部模仿”。它的主題一般不能太短，相對比較完整一些。如果模仿聲部對開始聲部陳述的音樂材料連續不斷地進行模仿，那就稱其為“卡農式模仿”。卡農式模仿的主題可長可短，根據情況而定。由于模仿復調中主題在各個聲部的依次進入，模仿復調賦予了音樂不斷發展的性質，因此它與支聲復調的不同之處在于每個瞬間都與其他聲部形成對比。

以上分別介紹了復調音樂的各種類型，但我們知道無論是單純的主調音樂還是復調音樂它都融合了多種寫作手法，所以我們不能孤立地去分析和研究，這不像我們在學習階段會單獨練習某一種寫作技巧，很多作品都是以一種綜合的寫作手法來表現音樂形象的。總之，無論是哪種復調手法，由于聲部的組合方式多種多樣，因而它們具體的類別也十分之多，在此不能詳細論述，只是從學習者的角度出發，對一些容易混淆的概念加以解釋和重點地強調，希望對他們有所幫助。

復對位、可動對位和繁復對位

西歐復調音樂完整教學體系中的單對位與復對位、模仿與卡農和賦格的復調音樂技術仍然是我國音樂院校專業復調音樂教學的主要教材。在此需要正確地區分復對位、可動對位和繁復對位這三者的概念，以免造成學習者的困惑與不解。一些學習者認為復對位就是繁復對位的簡稱也叫可動對位，其實這種認識是不正確的。它們三這是一種包含的關系：繁復對位包含可動對位，可動對位包含復對位。

A.復對位（Double counterpoint）：就是除原來的結合方式外，各聲部之間可以上下移動轉換并保持良好縱向關系的對位，也稱轉位對位。這種結合方式僅指上下聲部之間、在縱向上按一定的技術要求，可以相互交換位置，其各自的旋律不變，如果是二聲部復對位就叫二重對位，三聲部叫三重對位，以此類推……

其圖示為：

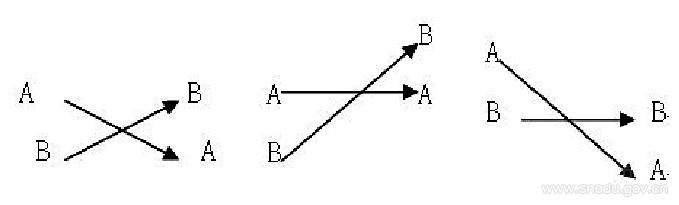
B.可動對位：指的是在對位音樂寫作中，除原來的結合方式外，各聲部間可以在縱向空間和橫向時間上加以變動而旋律本身不變的對位。復對位屬于縱向可動對位。

橫向可動對位是指兩個對比旋律縱向上不改變，而橫向進入的時間發生變化。圖示是：

原型 變形 1 變形2

縱橫可動對位是把縱向可動對位與橫向可動對位相結合而成。圖示是：

原型 變形 1 變形2

C.繁復對位：指的是在對位音樂寫作中，除原來的結合方式外，還可以采用它們的新的結合（變奏的一種方式）的對位。它是復調音樂體系中最復雜的寫作技術，包括有：1)可動對位： a縱向的垂直的 b橫向水平的 c縱橫可動對位；2)附加三、六度平形聲部的；3)倒映對位： a縱向的倒映對位 b橫向的倒映對位（也叫逆行） c二重倒映對位（也叫倒映逆行）；4）無終卡農和卡農模進等。

因此只有正確地理解和認識它們的概念，才能更加清楚地進行寫作和研究。

以上是本人在教學中發現學生容易搞混和出錯的一些概念和問題，在此匯總到一起加以簡單的解釋和重點的強調，供初學者參考，希望對他們學習復調會有所幫助。

參考文獻：

[1]于蘇賢.復調音樂教程[M]. 上海. 上海音樂出版社，2007.

[2]陳銘志.復調音樂寫作教程[M].北京.人民音樂出版社，1992.

[3]陳銘志.復調論文集[M].上海:上海音樂出版社，2002.

[4]林華.復調音樂簡明教程[M].上海:上海音樂學院出版社，2006.

[5]楊通八，張韻璇.和聲復調文集[M]. 上海:上海音樂出版社，2004.

[6]王安國主編.多聲部音樂分析與寫作[M].上海:上海音樂出版社，北京:人民音樂出版社，2007.

[7]饒余燕.關于復對位、可動對位和反復對位[D].復調音樂學術研討會論文集,2007.