最近兩年來，筆者對數(shù)學(xué)課堂“導(dǎo)學(xué)”進(jìn)行了探索與實踐，總結(jié)了以“思維導(dǎo)學(xué)”開展初中數(shù)學(xué)課堂教學(xué)的一些新途徑，取得了一定的成效。下面，就結(jié)合自己的探索和一點感悟，談?wù)劤踔袛?shù)學(xué)課堂中的“思維導(dǎo)學(xué)”。

一、初中數(shù)學(xué)課堂教學(xué)的呼喚——思維導(dǎo)學(xué)的必要性

（1）什么是思維導(dǎo)學(xué)。“導(dǎo)”，即“引導(dǎo)”之意；“學(xué)”即“學(xué)習(xí)”。所謂導(dǎo)學(xué)，通俗地說，就是引導(dǎo)學(xué)習(xí)。思維導(dǎo)學(xué)，是指在課堂教學(xué)中，通過創(chuàng)造條件發(fā)展并優(yōu)化學(xué)生的思維，以引導(dǎo)學(xué)生掌握學(xué)習(xí)的方法與策略，從而完成課堂教學(xué)任務(wù)的一種教學(xué)模式。

（2）思維導(dǎo)學(xué)的必要性。現(xiàn)代教學(xué)論認(rèn)為，教學(xué)過程不是單純的傳授和學(xué)習(xí)知識的過程，而是促進(jìn)學(xué)生全面發(fā)展的過程。從初中數(shù)學(xué)教學(xué)過程來說，數(shù)學(xué)知識和技能的掌握與思維能力的發(fā)展是密不可分的。一方面，學(xué)生在理解和掌握數(shù)學(xué)知識的過程中，不斷地運(yùn)用著各種思維方法和形式，如比較、分析、綜合、抽象、概括、判斷、推理；另一方面，在學(xué)習(xí)數(shù)學(xué)知識時，又為運(yùn)用思維方法和形式提供了具體的內(nèi)容和材料。所以，學(xué)生的思維需要教師的激發(fā)與培養(yǎng)，進(jìn)而達(dá)到發(fā)展與優(yōu)化。

二、提供條件，拓寬眼界——思維導(dǎo)學(xué)的實施策略

（1）提供條件，發(fā)展思維。數(shù)學(xué)知識和教學(xué)不只是為培養(yǎng)學(xué)生思維能力提供有利的條件，還需要在教學(xué)時有意識地充分利用這些條件，并且根據(jù)學(xué)生年齡特點有計劃地加以培養(yǎng)，才能達(dá)到預(yù)期的目的。

案例1：課外興趣小組活動時，我出示了如下問題：

如圖1，已知四邊形ABCD中，AC平分∠DAB，∠DAB=600，∠B與∠D互補(bǔ)，求證AB+AD= AC 。

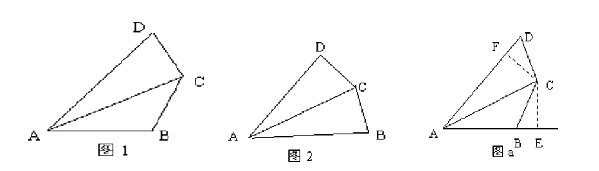
學(xué)生們反復(fù)探索，不得其解。

師說：“若將四邊形ABCD特殊化，看如何解決該問題？”

①如圖2，若增加條件：“∠B=∠D”，則可證AB+AD=AC。（請你完成此證明）

②受到①的啟發(fā)，若添加如圖a所示的輔助線：過C點分別作AB、AD的垂線，垂足分別為E、F。（請你補(bǔ)全原問題的證明）

通過對例題的分析與引導(dǎo)，讓學(xué)生經(jīng)歷“學(xué)”的認(rèn)知過程：從特殊出發(fā)，進(jìn)行推理或判斷，再對一般情形作出猜想或判斷。自始至終滲透了數(shù)學(xué)思想和方法，只有在①中深刻思考、充分理解的前提下，去尋找它們特殊和一般的必然聯(lián)系，形成解題的思路,才能拓寬學(xué)生的眼界，優(yōu)化他們的思維方法，培養(yǎng)學(xué)生的思維能力。

（2）拓寬眼界，優(yōu)化思維。新課標(biāo)對初中數(shù)學(xué)課堂教學(xué)的要求是：使學(xué)生獲得對數(shù)學(xué)理解的同時，在思維能力、情感態(tài)度與價值觀等多方面得到進(jìn)步和發(fā)展。由此可見，在數(shù)學(xué)教學(xué)中對思維培養(yǎng)和訓(xùn)練的重要性。那么，要開展數(shù)學(xué)課堂的“導(dǎo)學(xué)”教學(xué)，就要重視對學(xué)生思維的導(dǎo)學(xué)。

案例2：在學(xué)完全等三角形的判定方法后,出示這樣一個命題：“求證：有兩邊和其中一邊上的高對應(yīng)相等的兩個銳角三角形全等。”學(xué)生很容易證明,但是僅僅會證明對于發(fā)展中的學(xué)生來說還遠(yuǎn)遠(yuǎn)不夠。在課堂教學(xué)中，可以用如下幾個問題引導(dǎo)學(xué)生進(jìn)行更深層次的探索:

①將上述命題中的“高”改為“中線”,又怎樣證明?

②將上述命題中的“高”改為“角平分線”,又怎么證明?

③將命題中“其中一邊上的高”改為“第三邊上的高”,又怎么證明?

④將③中的“高”改為“中線”或者“角平分線”,又如何?

⑤將③中的“銳角三角形”改為“三角形”,結(jié)論還成立嗎?

通過這些問題的引導(dǎo)，使學(xué)生從更深刻的層次、更廣闊的角度對問題進(jìn)行再認(rèn)識，再提高，實現(xiàn)“導(dǎo)學(xué)”的有效性。

總之，數(shù)學(xué)課堂的思維導(dǎo)學(xué)，實質(zhì)上就是對學(xué)生的學(xué)習(xí)潛能、思維能力進(jìn)行發(fā)展與優(yōu)化的導(dǎo)學(xué)。只要教師能夠依據(jù)新課程標(biāo)準(zhǔn)的理念，從學(xué)生的實際出發(fā)，科學(xué)設(shè)計教學(xué)內(nèi)容，并運(yùn)用一定的導(dǎo)學(xué)策略，就一定能夠有效發(fā)展學(xué)生的思維能力，從而開辟出數(shù)學(xué)課堂教學(xué)的一片新天地。